
【题目】已知a,b,c为正数,满足如下两个条件:
a+b+c=32 ①![]() ②
②
是否存在以 ![]() ,
, ![]() ,
, ![]() 为三边长的三角形?如果存在,求出三角形的最大内角.
为三边长的三角形?如果存在,求出三角形的最大内角.
【答案】解法1:将①②两式相乘,得 ![]() ,
,
即: ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
即 ![]() ,
,
所以b﹣c+a=0或c+a﹣b=0或c﹣a+b=0,
即b+a=c或c+a=b或c+b=a.
因此,以 ![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.
解法2:结合①式,由②式可得 ![]() ,
,
变形,得 ![]() ③
③
又由①式得(a+b+c)2=1024,即a2+b2+c2=1024﹣2(ab+bc+ca),
代入③式,得 ![]() ,
,
即abc=16(ab+bc+ca)﹣4096.(a﹣16)(b﹣16)(c﹣16)=abc﹣16(ab+bc+ca)+256(a+b+c)﹣163=﹣4096+256×32﹣163=0,
所以a=16或b=16或c=16.
结合①式可得b+a=c或c+a=b或c+b=a.
因此,以 ![]() ,
, ![]() ,
, ![]() 为三边长可构成一个直角三角形,它的最大内角为90°.
为三边长可构成一个直角三角形,它的最大内角为90°.
【解析】解法一:根据已知,将两式相乘,运用平方差公式、完全平方式、提取公因式将乘积分解为 ![]() .再根据每个因式都可能等于零,及勾股定理,判断三角形为直角三角形.最大角度也就是90°
.再根据每个因式都可能等于零,及勾股定理,判断三角形为直角三角形.最大角度也就是90°
解法二:将①式变形代入,求出a、b、c的值,再利用勾股定理,判断三角形的为直角三角形.最大角度也就是90°.本题考查因式分解的应用.解决本题的关键是运用因式分解、等式变形求出a、b、c三角形三边的关系
【考点精析】利用勾股定理的逆定理和因式分解的应用对题目进行判断即可得到答案,需要熟知如果三角形的三边长a、b、c有下面关系:a2+b2=c2,那么这个三角形是直角三角形;因式分解是整式乘法的逆向变形,可以应用与数字计算、求值、整除性问题、判断三角形的形状、解方程.


科目:初中数学 来源: 题型:
【题目】小明去超市买三种商品.其中丙商品单价最高.如果购买3件甲商品、2件乙商品和1件丙商品,那么需要付费20元,如果购买4件甲商品,3件乙商品和2件丙商品,那么需要付费32元.
(1)如果购买三种商品各1件,那么需要付费多少元?
(2)如果需要购买1件甲商品,3件乙商品和2件丙商品,那么小明至少需多少钱才能保证一定能全部买到?(结果精确到元)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若a,b,c是直角三角形的三条边长,斜边c上的高的长是h,给出下列结论:
①以a2,b2,c2的长为边的三条线段能组成一个三角形;②以 ![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以
的长为边的三条线段能组成一个三角形;③以a+b,c+h,h的长为边的三条线段能组成直角三角形;④以 ![]() ,
, ![]() ,
, ![]() 的长为边的三条线段能组成直角三角形,正确结论的序号为 .
的长为边的三条线段能组成直角三角形,正确结论的序号为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】三个同学对问题“若方程组 ![]() 的解是
的解是 ![]() ,求方程组
,求方程组 ![]() 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请完成下列题目:
(1)如图①所示,P是等边△ABC内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转60°得△BCQ,连接PQ.若PA2+PB2=PC2,证明∠PQC=90°.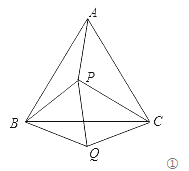
(2)
如图②所示,P是等腰直角△ABC(∠ABC=90°)内的一点,连接PA、PB、PC,将△BAP绕B点顺时针旋转90°得△BCQ,连接PQ.当PA、PB、PC满足什么条件时,∠PQC=90°?请说明
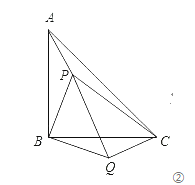
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在数学活动课上,老师和同学们判断一个四边形窗框是否为菱形,下面是某合作小组的4位同学拟定的方案,其中正确的是( )
A. 测量对角线是否相互垂直
B. 测量两组对边是否分别相等
C. 测量四个角是否相等
D. 测四条边是否相等
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,把直线y=x向左平移一个单位长度后,所得直线的解析式为( )
A. y=x+1 B. y=x-1 C. y=x D. y=x-2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com