
【题目】三个同学对问题“若方程组 ![]() 的解是
的解是 ![]() ,求方程组
,求方程组 ![]() 的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
的解.”提出各自的想法.甲说:“这个题目好象条件不够,不能求解”;乙说:“它们的系数有一定的规律,可以试试”;丙说:“能不能把第二个方程组的两个方程的两边都除以3,通过换元替换的方法来解决”.参考他们的讨论,你认为这个题目的解应该是 .
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某工厂计划生产A、B两种产品共50件,需购买甲、乙两种材料.生产一件A产品需甲种材料30千克、乙种材料10千克;生产一件B产品需甲、乙两种材料各20千克.经测算,购买甲、乙两种材料各1千克共需资金40元,购买甲种材料2千克和乙种材料3千克共需资金105元.
(1)甲、乙两种材料每千克分别是多少元?
(2)现工厂用于购买甲、乙两种材料的资金不超过38000元,且生产B产品不少于28件,问符合条件的生产方案有哪几种?
(3)在(2)的条件下,若生产一件A产品需加工费200元,生产一件B产品需加工费300元,应选择哪种生产方案,使生产这50件产品的成本最低?(成本=材料费+加工费)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于A,B两点,与y轴交于点C,且OA=OC,则下列结论:①abc<0;②![]() ;③ac﹣b+1=0;④OAOB=﹣
;③ac﹣b+1=0;④OAOB=﹣![]() .其中正确结论的序号是 .
.其中正确结论的序号是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】热气球的探测器显示,从热气球底部A处看一栋高楼顶部的俯角为30°,看这栋楼底部的俯角为60°,热气球A处与地面距离为420米,求这栋楼的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列函数关系中,属于正比例函数关系的是( )
A.圆的面积与它的半径
B.面积为常数S时矩形的长y与宽x
C.路程是常数时,行驶的速度v与时间t
D.三角形的底边是常数a时它的面积S与这条边上的高h
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小明骑自行车上学,一开始以某一恒定的速度行驶,但行驶至途中自行车发生了故障,只好停下来修车,车修好后,因怕耽误了上课,他比修车前加快了骑车的速度,下面四幅图中最能反映小明这段行程的是( )
A.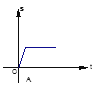
B.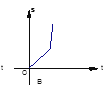
C.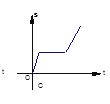
D.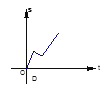
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠C=90°,∠ABC=30°,AB=8,将△ABC沿CB向右平移得到△DEF.若四边形ABED的面积等于8,则平移距离等于( )
A.2
B.4
C.8
D.16
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com