练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】如图，已知∠AOB＝40°，∠BOC＝3∠AOB，OD平分∠AOC，求∠COD的度数．

    解：∵∠BOC＝3∠　 ，∠AOB＝40°，

    ∴∠BOC＝　 °

    ∴∠AOC＝　 　+　

    ∴∠AOC＝160°

    ∵OD平分∠AOC

    ∴∠COD＝　 ＝　 °．

    【答案】AOB；120；∠AOB；∠BOC；∠AOC；80．

    【解析】

    根据角的倍数关系，得∠BOC＝120°，进而得∠AOC＝160°，根据角平分线的定义，即可得到答案．

    ∵∠BOC＝3∠AOB，∠AOB＝40°，

    ∴∠BOC＝120°，

    ∴∠AOC＝∠AOB+∠BOC

    ∴∠AOC＝160°

    ∵OD平分∠AOC

    ∴∠COD＝∠AOC＝80°．

    故答案是：AOB；120；∠AOB；∠BOC；∠AOC；80．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某汽车出发前油箱内有油42L，行驶若干小时后，在途中加油站加油若干升．邮箱中剩余油量Q（L）与行驶时间t（h）之间的函数关系如图所示．

    （1）汽车行驶　 　h后加油，加油量为　 　L；

    （2）求加油前油箱剩余油量Q与行驶时间t之间的函数关系式；

    （3）如果加油站离目的地还有200km，车速为40km/h，请直接写出汽车到达目的地时，油箱中还有多少汽油？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】公元3世纪初，我国学家赵爽证明勾定理的图形称为“弦图”．1876年美国总统Garfeild用图1（点C、点B、点C′三点共线）进行了勾股定理的证明．△ACB与△BC′B′是一样的直角三角板，两直角边长为a，b，斜边是c．请用此图1证明勾股定理．

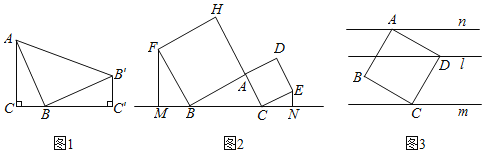
    拓展应用l：如图2，以△ABC的边AB和边AC为边长分别向外做正方形ABFH和正方形ACED，过点F、E分别作BC的垂线段FM、EN，则FM、EN、BC的数量关系是怎样？直接写出结论　 　．

    拓展应用2：如图3，在两平行线m、n之间有一正方形ABCD，已知点A和点C分别在直线m、n上，过点D作直线l∥n∥m，已知l、n之间距离为1，l、m之间距离为2．则正方形的面积是　 　．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

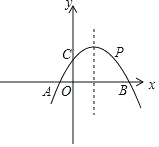
    【题目】如图，已知抛物线y＝ax2+bx+1与x轴分别交于A(﹣1，0)，B(3，0)，与y轴交于点C．

    (1)求抛物线解析式；

    (2)在直线BC上方的抛物线上有点P，使△PBC面积为1，求出点P的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】红星中学九年级(1)班三位教师决定带领本班名学生利用假期去某地旅游，枫江旅行社的收费标准为：教师全价，学生半价；而东方旅行社不管教师还是学生一律八折优惠，这两家旅行社的全价都是500元。

    (1)用含的式子表示三位教师和位学生参加这两家旅行社所需的费用各是多少元；

    (2)如果=50时，请你计算选择哪一家旅行社较为合算？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】为弘扬中华传统文化，某校组织八年级800名学生参加汉字听写大赛为了解学生整体听写能力，从中抽取部分学生的成绩（得分取正整数，满分为100分）进行统计分析，得到如下所示的模数分布表：

    分数段

    50.5﹣60.5

    60.5﹣70.5

    70.5﹣80.5

    80.5﹣90.5

    90.5﹣100.5

    频数

    16

    30

    50

    m

    24

    所占百分比

    8%

    15%

    25%

    40%

    n

    请根据尚未完成的表格，解答下列问题：

    （1）本次抽样调查的样本容量为　 ，表中m＝　 ．n=　 ；

    （2）补全图中所示的频数分布直方图；

    （3）若成绩超过80分为优秀，则该校八年级学生中汉字听写能力优秀的约有多少人？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知点A（4，0）及在第一象限的动点P（x，y），且x+y=5，0为坐标原点，设△OPA的面积为S．

    （1）求S关于x的函数表达式；

    （2）求x的取值范围；

    （3）当S=4时，求P点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，已知AC⊥BC，BD⊥AD，AC与BD交于O，AC=BD．

    求证：△OAB是等腰三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系上有点A(1，0)，点A第一次跳动至点，第二次点跳动至点第三次点跳动至点，第四次点跳动至点……，依此规律跳动下去，则点与点之间的距离是（ ）

    A. 2017B. 2018C. 2019D. 2020

    查看答案和解析>>

    同步练习册答案