
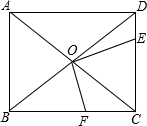
 如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于O,E为DC的一点,过点O作OF⊥OE交BC于F.记d=$\sqrt{D{E^2}+B{F^2}}$,则关于d的正确的结论是( )
如图,在矩形ABCD中,AB=6,BC=8,AC与BD相交于O,E为DC的一点,过点O作OF⊥OE交BC于F.记d=$\sqrt{D{E^2}+B{F^2}}$,则关于d的正确的结论是( )| A. | d=5 | B. | d<5 | C. | d≤5 | D. | d≥5 |
分析 延长EO交AB于G,根据ASA可证△DOE≌△BOG,可得BG=DE,则d=$\sqrt{D{E^2}+B{F^2}}$,即为FG的长;过O点作OH⊥AB于H,OI⊥BC于I,可得△OHG∽△OFI,设BG=x,用x表示出BF,再根据函数的最值即可求解.
解答 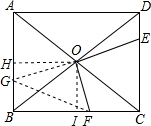 解:延长EO交AB于G,连结GF.
解:延长EO交AB于G,连结GF.
∵四边形ABCD是矩形,
∴OB=OD,AB∥CD,
∴∠OBG=∠OED,
在△DOE与△BOG中,
$\left\{\begin{array}{l}{∠OBG=∠ODD}\\{OB=OD}\\{∠BOG=∠DOE}\end{array}\right.$,
∴△DOE≌△BOG(ASA),
∴BG=DE,
∴d=$\sqrt{D{E^2}+B{F^2}}$=FG;
过O点作OH⊥AB于H,OI⊥BC于I,可得△OHG∽△OFI,
设BG=x,则HG=3-x,
则IF:HG=4:3,
IF=4-$\frac{4}{3}$x,
BF=4+4-$\frac{4}{3}$x=8-$\frac{4}{3}$x,
d=$\sqrt{{x}^{2}+(8-\frac{4}{3}x)^{2}}$=$\sqrt{\frac{25}{9}(x-\frac{96}{25})^{2}+\frac{576}{25}}$,
∵0≤x≤3,
∴当x=3时,d最小为5,即d≥5.
故选:D.
点评 考查了矩形的性质,全等三角形的判定与性质,勾股定理,解题的关键是设BG=x,用x表示出BF.


 活力课时同步练习册系列答案
活力课时同步练习册系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
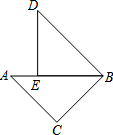 如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )
如图,△ABC和△DBE都是等腰直角三角形,点E在AB上,若△ABC经旋转后能与△DBE重合,则旋转中心为( )| A. | 点A | B. | 点B | C. | 点C | D. | 点E |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a≥2 | B. | a≥-2 | C. | a≤2 | D. | a≤-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com