
【题目】如图,将□ABCD的边DC延长至点E,使得CE=DC,连结AE,AC,BE,且AE交BC于点F.
(1)求证:AE与BC互相平分;
(2)若∠AFC=2∠D,AD=10.
①求证:四边形ABEC是矩形;
②连结FD,则线段FD的长度的取值范围为____.

【答案】(1)见解析;(2)①见解析;②5<FD<15.
【解析】
(1)利用平行四边形的性质,易证AB∥CD,AB=CD,再由CE=CD,可证AB=CE,再利用一组对边平行且相等的四边形是平行四边形,可证得四边形ABEC是平行四边形,然后利用平行四边形的对角线互相平分,可证得结论.
(2)①利用平行四边形的对角相等,可证∠D=∠ABC,再利用三角形外角的性质及∠AFC=2∠D,易证∠AFC=2∠ABC=∠ABC+∠BAF,就可推出∠ABC=∠BAF,利用等角对等边,可知FA=FB ,就可证得平行四边形ABEC的对角线相等,即可证得结论;②由平行四边形的性质和矩形的性质可求出AF的长,再利用三角形的三边关系定理就可求出DF的取值范围.
(1)证明:∵平行四边形ABCD
∴AB∥CD,AB=CD,CD=CE
∴AB∥CE,AB=CE
∴得□ABEC
∴AE与BC互相平分
(2)①∵∠D=∠ABC,∠AFC=2∠D
∴∠AFC=2∠ABC
∵∠ABC+∠BAF=∠AFC
∴ ∠ABC=∠BAF
∴ FA=FB
∴ AE=BC
∴四边形ABEC是矩形.
②连接DF

∵平行四边形ABCD
∴BC=AD=10
∵矩形ABEC
∴AF=BF=10÷2=5
在△AFD中,AD-AF<DF<AD+AF
∴10-5<DF<10+5
即5<DF<15


科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,E是AB边上一点,且∠A=∠EDF=60°,有下列结论:①AE=BF;②△DEF是等边三角形;③△BEF是等腰三角形;④∠ADE=∠BEF,其中结论正确的个数是( )
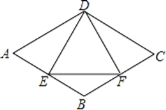
A.3
B.4
C.1
D.2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:甲乙两车分别从相距300千米的A、B两地同时出发相向而行,其中甲到达B地后立即返回,如图是它们离各自出发地的距离y(千米)与行驶时间x(小时)之间的函数图象.

(1)求甲车离出发地的距离y甲(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(2)它们出发![]() 小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
小时时,离各自出发地的距离相等,求乙车离出发地的距离y乙(千米)与行驶时间x(小时)之间的函数关系式,并写出自变量的取值范围;
(3)在(2)的条件下,求它们在行驶的过程中相遇的时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程x2+2019x+m=0与x2+mx+2019=0有且只有一个公共根,m的值为( )
A. 2019B. -2019C. 2020D. -2020
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核,甲、乙、丙各项得分如下表:
考核人员 | 笔试 | 面试 | 体能 | 平均分 |
甲 | 83 | 79 | 90 | 84 |
乙 | 86 | 80 | x | 80 |
丙 | 80 | 90 | 73 | y |
(1)根据表格中的数据信息,求得x=_____;y=____.
(2)该公司规定:笔试、面试、体能得分分别不得低于80分,80分,70分,并按50%,30%,20%的比例计入总分.请你根据规定,计算说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(6,4)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是( )

A. (2,12)
B. (﹣2,0)
C. (2,12)或(﹣2,0)
D. (12,2)或(﹣2,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
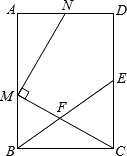
【题目】如图,在矩形ABCD中,E为CD的中点,F为BE上的一点,连结CF并延长交AB于点M,MN⊥CM交射线AD于点N.
(1)当F为BE中点时,求证:AM=CE;
(2)若![]() =2,求
=2,求![]() 的值;
的值;
(3)若![]() =n,当n为何值时,MN∥BE?
=n,当n为何值时,MN∥BE?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】雾霾天气严重影响市民的生活质量。在今年寒假期间,某校九年级一班的综合实践小组学生对“雾霾天气的主要成因”随机调查了所在城市部分市民,并对调查结果进行了整理,绘制了下图所示的不完整的统计图表:
组别 | 雾霾天气的主要成因 | 百分比 |
A | 工业污染 | 45% |
B | 汽车尾气排放 |
|
C | 炉烟气排放 | 15% |
D | 其他(滥砍滥伐等) |
|
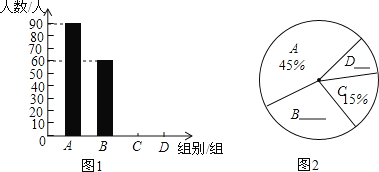
请根据统计图表回答下列问题:
(1)本次被调查的市民共有多少人?并求![]() 和
和![]() 的值;
的值;
(2)请补全条形统计图,并计算扇形统计图中扇形区域![]() 所对应的圆心角的度数;
所对应的圆心角的度数;
(3)若该市有100万人口,请估计市民认为“工业污染和汽车尾气排放是雾霾天气主要成因”的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题满分7分)已知关于x的方程![]() 有两个不相等的实数根.
有两个不相等的实数根.
(1)求k的取值范围;
(2)是否存在实数k,使此方程的两个实数根的倒数和等于0?若存在,求出k的值;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com