
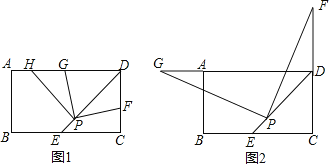
����Ŀ����֪�ھ���ABCD�У���ADC��ƽ����DE��BC�����ڵ�ֱ�߽��ڵ�E����P���߶�DE��һ���㣨����EP��PD��
��1����ͼ1������F��CD���ϣ�����D�غϣ�������DPF�Ƶ�P��ʱ����ת90���ǵ�����PD��PF�ֱ�����DA�ڵ�H��G��
����֤��PG=PF��
��̽����DF��DG��DP֮����������������ϵ����֤����Ľ��ۣ�
��2����չ����ͼ2������F��CD���ӳ����ϣ�����D�غϣ�������P��PG��PF��������DA�ڵ�G������Ϊ��1����DE��DG��DP֮���������ϵ�Ƿ���Ȼ������������������֤����������������д�������������������ϵʽ����˵�����ɣ�
���𰸡���1����֤������������DG+DF=![]() DP����2����������������ϵʽӦΪ��DG��DF=
DP����2����������������ϵʽӦΪ��DG��DF=![]() DP��
DP��
�������������������1������֤PG=PF����֤��HPG�ա�DPF����֪��DPH=��HPG������ת��֪��GPF=��HPD=90�㼰DEƽ�֡�ADC�á�HPDΪ����ֱ�������Σ�����DHP=��PDF=45�㡢PD=PH�����ɵ�֤��
���ɡ�HPDΪ����ֱ�������Σ���HPG�ա�DPF֪HD=![]() DP��HG=DF������DG+DF=DG+GH=DH���ɵã�
DP��HG=DF������DG+DF=DG+GH=DH���ɵã�
�����������2������P��PH��PD������DA�ڵ�H����֤��HPDΪ����ֱ�������οɵ�PH=PD��HD=![]() DP����֤��HPG�ա�DPF�ɵ�HG=DF������DH=DG-HG=DG-DF�ɵ�DG-DF=
DP����֤��HPG�ա�DPF�ɵ�HG=DF������DH=DG-HG=DG-DF�ɵ�DG-DF=![]() DP��
DP��
��1���١ߡ�GPF=��HPD=90�㣬��ADC=90�㣬
���GPH=��FPD��
��DEƽ�֡�ADC��
���PDF=��ADP=45�㣬
���HPDΪ����ֱ�������Σ�
���DHP=��PDF=45�㣬
�ڡ�HPG�͡�DPF�У�
��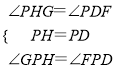 ��
��
���HPG�ա�DPF��ASA����
��PG=PF��
�ڽ��ۣ�DG+DF=![]() DP��
DP��
�ɢ�֪����HPDΪ����ֱ�������Σ���HPG�ա�DPF��
��HD=![]() DP��HG=DF��
DP��HG=DF��
��HD=HG+DG=DF+DG��
��DG+DF=![]() DP��
DP��
��2����������������ϵʽӦΪ��DG-DF=![]() DP��
DP��
��ͼ������P��PH��PD������DA�ڵ�H��
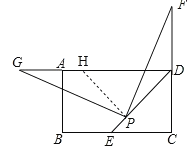
��PF��PG��
���GPF=��HPD=90�㣬
���GPH=��FPD��
��DEƽ�֡�ADC�����ھ���ABCD�У���ADC=90�㣬
���HDP=��EDC=45�㣬�õ���HPDΪ����ֱ�������Σ�
���DHP=��EDC=45�㣬��PH=PD��HD=![]() DP��
DP��
���GHP=��FDP=180��-45��=135�㣬
�ڡ�HPG�͡�DPF�У�
��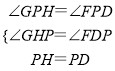
���HPG�ա�DPF��
��HG=DF��
��DH=DG-HG=DG-DF��
��DG-DF=![]() DP��
DP��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ABCD�У�AC��BD����O�㣬BE��AC��E��CF��BD��F�� 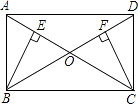
��֤��
��1����ACB=��DBC��
��2��BE=CF��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̵��һ����300Ԫ�����ʼDZ����ɣ��ڶ�������300Ԫ�����ÿ�ʼDZ��������ÿ���Ľ����ǵ�һ�ν��۵�![]() �������������ȵ�һ������25����
�������������ȵ�һ������25����
��1�����һ��ÿ���ʼDZ��Ľ����Ƕ���Ԫ��
��2����Ҫ�������ι����ıʼDZ���ͬһ�۸�ȫ��������Ϻ����������450Ԫ����ÿ���ʼDZ����ۼ������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��O�İ뾶Ϊ2��ֱ��l����һ��P����PO=2����ֱ��l���O��λ�ù�ϵ�ǣ� ��
A.����
B.����
C.���������
D.���л��ཻ
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������������ǽʱ��������ϸ����ǽ������֮����һ�������ߣ�ʹ����ÿһ��ש��һ��ֱ���ϣ����������̺�����ѧԭ����__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��1��2m��x+m��1��������y��x���������С�����Һ�����ͼ���������������ޣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������߶��У�����������ε��ǣ� ��
A. 1��2��3 B. 1��2��4 C. 3��4��5 D. 4��4��8
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������������ε����֮��Ϊ1��4�������ǵ��ܳ�֮��Ϊ�� ��
A.1��2B.1��4C.1��5D.1��16
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����A(��4����5)����B(��6����5)����AB����( )
A. 4 B. 2 C. 5 D. 3
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com