
| A. | m•tanα•cosα | B. | m•cotα•cosα | C. | $\frac{m•tanα}{cosα}$ | D. | $\frac{m•tanα}{sinα}$ |
分析 根据在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,可以用含m和α的三角函数值表示出CD,通过角相等,它们的三角函数值也相等,可以解答本题.
解答 解:∵在Rt△ABC中,∠C=90°,CD是高,如果AD=m,∠A=α,
∴tanα=$\frac{CD}{AD}=\frac{CD}{m}$,
∴CD=m•tanα,
∵∠ACB=∠A+∠B=90°,∠BDC=∠B+∠BCD=90°,∠A=α,
∴∠BCD=α,
∴cos∠BCD=$\frac{CD}{BC}=\frac{m•tanα}{BC}$,
即cos$α=\frac{m•tanα}{BC}$,
BC=$\frac{m•tanα}{cosα}$.
故选C.
点评 本题考查解直角三角函数,解题的关键是明确各个三角函数值的意义,利用转化的思想找到所求问题需要的条件.


 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案 周周清检测系列答案
周周清检测系列答案 轻巧夺冠周测月考直通高考系列答案
轻巧夺冠周测月考直通高考系列答案科目:初中数学 来源: 题型:选择题
| A. | 3a-3=5b-4 | B. | 3a+b=6b-1 | C. | 3ac=5bc-1 | D. | b=$\frac{3a+1}{5}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
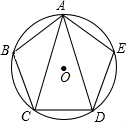 如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)
如图,正五边形ABCD内接于⊙O,连接对角线AC,AD,则下列结论:①BC∥AD;②∠BAE=3∠CAD;③△BAC≌△EAD;④AC=2CD.其中判断正确的是①②③.(填序号)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com