
【题目】如图,在菱形ABCD中,AB=6,∠DAB=60°,AE分别交BC、BD于点E、F,若CE=2,连接CF.以下结论:①∠BAF=∠BCF; ②点E到AB的距离是2![]() ; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
; ③S△CDF:S△BEF=9:4; ④tan∠DCF=3/7. 其中正确的有()
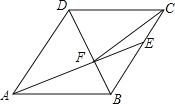
A. 4个 B. 3个 C. 2个 D. 1个
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】2020年是5G爆发元年,三大运营商都在政策的支持下,加快着5G建设的步伐.某通信公司实行的5G畅想套餐,部分套餐资费标准如下:
套餐类型 | 月费(元/月) | 套餐内包含内容 | 套餐外资费 | ||
国内数据流量(GB) | 国内主叫(分钟) | 国内流量 | 国内主叫 | ||
套餐1 | 128 | 30 | 200 | 每5元1GB,用满3GB后每3元1GB,不足部分按照0.03/元MB收取 | 0.19元/分钟 |
套餐2 | 158 | 40 | 300 | ||
套餐3 | 198 | 60 | 500 | ||
套餐4 | 238 | 80 | 600 | ||
小武每月大约使用国内数据流量49GB,国内主叫350分钟,若想使每月付费最少,则他应预定的套餐是( )
A.套餐1B.套餐2C.套餐3D.套餐4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定,以二次函数![]() 的二次项系数
的二次项系数![]() 的2倍为一次项系数,一次项系数
的2倍为一次项系数,一次项系数![]() 为常数项构造的一次函数
为常数项构造的一次函数![]() 叫做二次函数
叫做二次函数![]() 的“子函数”,反过来,二次函数
的“子函数”,反过来,二次函数![]() 叫做一次函数
叫做一次函数![]() 的“母函数”.
的“母函数”.
(1)若一次函数![]() 是二次函数
是二次函数![]() 的“子函数”,且二次函数经过点
的“子函数”,且二次函数经过点![]() ,求此二次函数的解析式.
,求此二次函数的解析式.
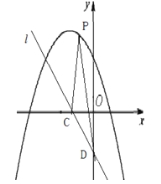
(2)如图,已知二次函数![]() 的“子函数”图象直线
的“子函数”图象直线![]() 与
与![]() 轴、
轴、![]() 轴交于
轴交于![]() 、
、![]() 两点,点
两点,点![]() 是直线
是直线![]() 上方的抛物线上任意一点,求
上方的抛物线上任意一点,求![]() 的面积的最大值.
的面积的最大值.
(3)已知二次函数![]() 与它的“子函数”
与它的“子函数”![]() 的函数图象有两个交点
的函数图象有两个交点![]() ,
,![]() ,且
,且![]() ,求
,求![]() 的值;
的值;
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】自从开展“创建全国文明城区“工作以来,门头沟区便掀起了“门头沟热心人“志愿服务的热潮,区教委也号召各校学生积极参与到志愿服务当中.为了解甲、乙两所学校学生一周志愿服务情况,从这两所学校中各随机抽取40名学生,分别对他们一周的志愿服务时长(单位:分钟)数据进行收集、整理、描述和分析.下面给出了部分信息:
a.甲校40名学生一周的志愿服务时长的扇形统计图如图(数据分成6组:![]() ):
):
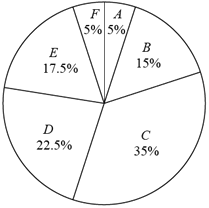
A:![]() B:
B:![]()
C:![]() D:
D:![]()
E:![]() F:
F:![]()
b.甲校40名学生一周志愿服务时长在![]() 这一组的是:
这一组的是:
60 60 62 63 65 68 70 72 73 75 75 76 80 80
c.甲、乙两校各抽取的40名学生一周志愿服务时长的平均数、中位数、众数如下:
学校 | 平均数 | 中位数 | 众数 |
甲校 | 75 |
| 90 |
乙校 | 75 | 76 | 85 |
根据以上信息,回答下列问题:
(1)![]() _____________;
_____________;
(2)根据上面的统计结果,你认为____①_____所学校学生志愿服务工作做得好(填“甲“或“乙“),理由______②________________________________________________________;
(3)甲校要求学生一周志愿服务的时长不少于60分钟,如果甲校共有学生800人,请估计甲校学生中一周志愿服务时长符合要求的有_______人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进![]() ,
,![]() 两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
两种新型节能台灯共120盏,这两种台灯的进价和售价如表所示:
价格 类型 | 进价(元/盏) | 售价(元/盏) |
| 40 | 55 |
| 60 | 80 |
(1)若商场恰好用完预计进货款5500元,则应这购进两种台灯各多少盏?
(2)若商场规定![]() 型台灯的进货数量不超过
型台灯的进货数量不超过![]() 型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
型台灯数量的3倍,应怎样进货才能使商场在销售完这两种台灯时获得的毛利润最多?最多毛利润为多少元?(毛利润=销售收入-进货成本).
查看答案和解析>>
科目:初中数学 来源: 题型:
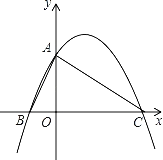
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象与y轴交于点A(0,4),与x轴负半轴交于B,与正半轴交于点C(8,0),且∠BAC=90°.
(1)求该二次函数解析式;
(2)若N是线段BC上一动点,作NE∥AC,交AB于点E,连结AN,当△ANE面积最大时,求点N的坐标;
(3)若点P为x轴上方的抛物线上的一个动点,连接PA、PC,设所得△PAC的面积为S.问:是否存在一个S的值,使得相应的点P有且只有2个?若有,求出这个S的值,并求此时点P的横坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
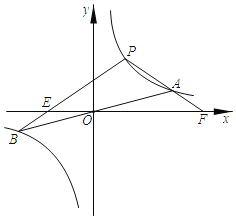
【题目】如图,双曲线y1=![]() 与直线y2=
与直线y2=![]() 的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=
的图象交于A、B两点.已知点A的坐标为(4,1),点P(a,b)是双曲线y1=![]() 上的任意一点,且0<a<4.
上的任意一点,且0<a<4.
(1)分别求出y1、y2的函数表达式;
(2)连接PA、PB,得到△PAB,若4a=b,求三角形ABP的面积;
(3)当点P在双曲线y1=![]() 上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
上运动时,设PB交x轴于点E,延长PA交x轴于点F,判断PE与PF的大小关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.为了解全国中学生视力的情况,应采用普查的方式
B.某种彩票中奖的概率是![]() ,买1000张这种彩票一定会中奖
,买1000张这种彩票一定会中奖
C.从2000名学生中随机抽取200名学生进行调查,样本容量为200名学生
D.从只装有白球和绿球的袋中任意摸出一个球,摸出黑球是确定事件
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某企业甲、乙两位员工的能力测试结果的网状图,以O为圆心的五个同心圆分别代表能力水平的五个等级由低到高分别赋分1至5分,由原点出发的五条线段分别指向能力水平的五个维度,网状图能够更加直观的描述测试者的优势和不足,观察图形,有以下几个推断:
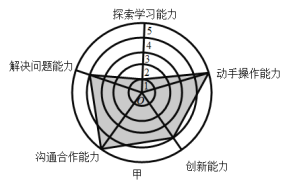
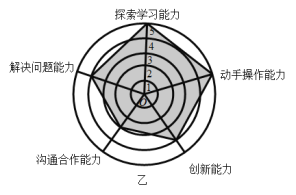
①甲和乙的动手操作能力都很强;
②缺少探索学习的能力是甲自身的不足;
③与甲相比乙需要加强与他人的沟通合作能力;
④乙的综合评分比甲要高.
其中合理的是( )
A.①③B.②④C.①②③D.①②③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com