
 把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个.
把数字按如图所示排列起来,从上开始,依次为第一行、第二行、第三行.中间用虚线围的一列,从上至下:第一个数为1,第二个数为5,第三个数为13,第四个数为25,…,则第十个数为181,数“2015”在第六十三行,从左边数第2个. 分析 中间用虚线围的一列,从上至下,相邻两个数都相差4,由此可求出第十个数;结合图形可得第(2n-1)行的第1个数为1+2+3+…+(2n-1),由此可得数“2016”是第六十三行的第1个数,再根据第(2n-1)行后一个数比前一个数少1,就可解决问题.
解答 解:中间用虚线围的一列,从上至下:
第一个数为1,
第二个数为5=1+4×1,
第三个数为13=1+4×1+4×2,
第四个数为25=1+4×1+4×2+4×3,
…,
则第十个数为1+4×1+4×2+4×3+…+4×9
=1+4(1+2+3+…+9)=1+4×$\frac{9(1+9)}{2}$=181;
有图可知:
第三行的第1个数为6=1+2+3,
第五行的第1个数为15=1+2+3+4+5,
第七行的第1个数为28=1+2+3+4+5+6+7,
…,
则第六十三行的第1个数为1+2+3+…+63=$\frac{63×(1+63)}{2}$=2016,
所以数“2015”在第六十三行,从左边起第2个.
故答案分别为181,六十三,2.
点评 本题属于规律探究题,关注相邻两个数之间的关系是解决本题的关键,在解决问题的过程中,用到了公式1+2+3+…+n=$\frac{n(n+1)}{2}$,应熟练掌握.


 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案科目:初中数学 来源: 题型:解答题
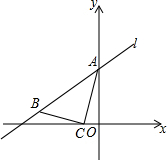 如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.
如图,直线l的表达式为y=kx+3(k>0),与y轴交于点A,点C在x轴的负半轴上,过点C作BC⊥AC交直线l于点B,且BC=CA,已知AC=$\sqrt{10}$,求k的值.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
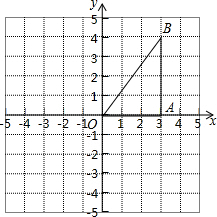 在10×10的网格纸上建立平面直角坐标系如图所示,在直角三角形ABO中,∠OAB=90°,且点B的坐标为(3,4).
在10×10的网格纸上建立平面直角坐标系如图所示,在直角三角形ABO中,∠OAB=90°,且点B的坐标为(3,4).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com