
如图,在平面直角坐标系中,△ABC的顶点A在x轴负半轴上,顶点C在x轴正半轴上,顶点B在第一象限,过点B作BD⊥y轴于点D,线段OA,OC的长是一元二次方程x2﹣12x+36=0的两根,BC=4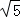 ,∠BAC=45°.
,∠BAC=45°.
(1)求点A,C的坐标;
(2)反比例函数y=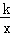 的图象经过点B,求k的值;
的图象经过点B,求k的值;
(3)在y轴上是否存在点P,使以P,B,D为顶点的三角形与以P,O,A为顶点的三角形相似?若存在,请写出满足条件的点P的个数,并直接写出其中两个点P的坐标;若不存在,请说明理由.
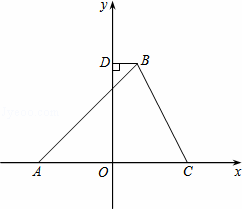
解:(1)解一元二次方程x2﹣12x+36=0,解得:x1=x2=6,
∴OA=OC=6,
∴A(﹣6,0),C(6,0);
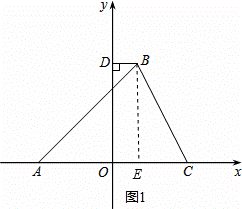
(2)如图1,过点B作BE⊥AC,垂足为E,
∵∠BAC=45°,
∴AE=BE,
设BE=x,
∵BC=4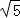 ,
,
∴CE=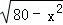 ,
,
∵AE+CE=OA+OC,
∴x+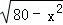 =12,
=12,
整理得:x2﹣12x+32=0,
解得:x1=4(不合题意舍去),x2=8
∴BE=8,OE=8﹣6=2,
∴B(2,8),
把B(2,8)代入y=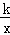 ,得k=16.
,得k=16.
(3)存在.
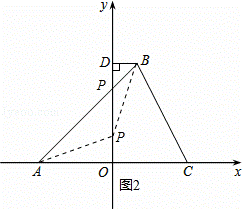
如图2,若点P在OD上,若△PDB∽△AOP,
则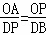 ,
,
即
解得:OP=2或OP=6
∴P(0,2)或P(0,6);
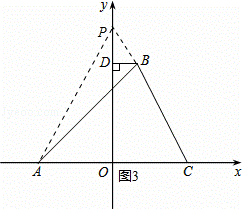
如图3,若点P在OD上方,△PDB∽△AOP,
则 ,
,
即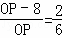 ,
,
解得:OP=12,
∴P(0,12);
如图4,若点P在OD上方,△BDP∽△AOP,
则 ,
,
即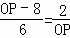 ,
,
解得:OP=4+2 或OP=4﹣2
或OP=4﹣2 (不合题意舍去),
(不合题意舍去),
∴P(0,4+2 );
);
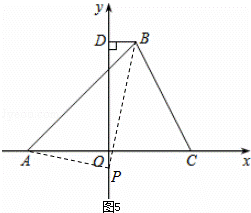
如图5,若点P在y轴负半轴,△PDB∽△AOP,
则 ,即
,即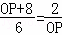 ,解得:OP=﹣4+2
,解得:OP=﹣4+2 或﹣4﹣2
或﹣4﹣2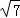 ,则P点坐标为(0,2
,则P点坐标为(0,2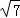 ﹣4)或(0,4+2
﹣4)或(0,4+2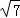 )(不合题意舍去).
)(不合题意舍去).
∴点P的坐标为:(0,2)或(0,6)或(0,12)或(0,4+2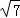 )或(0,2
)或(0,2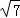 ﹣4).
﹣4).



科目:初中数学 来源: 题型:
(1)问题
如图1,在四边形ABCD中,点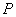 为
为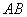 上一点,
上一点, 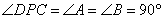 .
.
求证:AD·BC=AP·BP.
(2)探究
如图2,在四边形ABCD中,点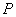 为
为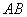 上一点,当
上一点,当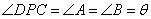 时,上述结论是否依然成立?说明理由.
时,上述结论是否依然成立?说明理由.
(3)应用
请利用(1)(2)获得的经验解决问题:
如图3,在△ABD中,AB=6,AD=BD=5, 点P以每秒1个单位长度的速度,由点A出发,沿边AB向点B运动,且满足∠CPD=∠A.设点P的运动时间为t(秒),当以 D为圆心,
D为圆心,
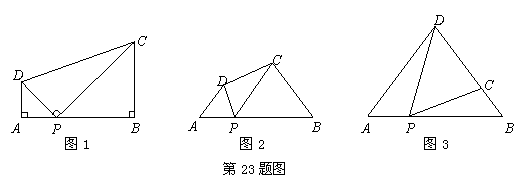 DC为半径的圆与AB相切时,求t的值.
DC为半径的圆与AB相切时,求t的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省九年级下学期第一次学情调研数学试卷(解析版) 题型:解答题
如图,在菱形ABCD中,AB=2,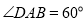 ,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.
,点E是AD边的中点,点M是AB边上一动点(不与点A重合),延长ME交射线CD于点N,连接MD,AN.

(1)求证:四边形AMDN是平行四边形;
(2)填空:①当AM的值为 时,四边形AMDN是矩形;
②当AM的值为 时,四边形AMDN是菱形。
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省扬州市江都区七校联谊九年级3月月考数学试卷(解析版) 题型:解答题
(14’)如图,在平面直角坐标系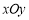 中,A、B为
中,A、B为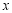 轴上两点,C、D为
轴上两点,C、D为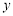 轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,
轴上的两点,经过点A、C、B的抛物线的一部分C1与经过点A、D、B的抛物线的一部分C2组合成一条封闭曲线,我们把这条封闭曲线称为“蛋线”.已知点C的坐标为(0,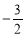 ),点M是抛物线C2:
),点M是抛物线C2: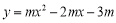 (
(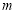 <0)的顶点.
<0)的顶点.
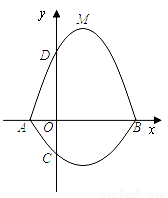
(1)求A、B两点的坐标;
(2)“蛋线”在第四象限上是否存在一点P,使得△PBC的面积最大?若存在,求出△PBC面积的最大值;若不存在,请说明理由;
(3)当△BDM为直角三角形时,求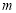 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2014-2015学年江苏省无锡市锡山区九年级上学期期末考试数学试卷(解析版) 题型:填空题
在-1,0,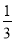 ,
,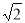 ,π,0.10110中任取一个数,取到无理数的概率是__________.
,π,0.10110中任取一个数,取到无理数的概率是__________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com