
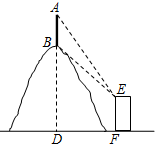
 如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)
如图,在观测点E测得小山上铁塔顶A的仰角为60°,铁塔底部B的仰角为45°.已知塔高AB=20m,观测点E到地面的距离EF=35m,求小山BD的高.(结果保留根号)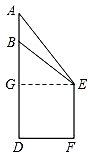 解:如图,过点E作EG⊥AD于点G.
解:如图,过点E作EG⊥AD于点G.| AG |
| EG |
| 3 |
| 3 |
| 3 |
| 20 | ||
|
| 3 |
| 3 |


科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
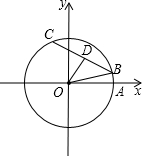 如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )
如图,在平面直角坐标系xOy中,以原点O为圆心的圆过点A(13,0),直线y=kx-3k+4与⊙O交于B、C两点,则弦BC的长的最小值为( )| A、22 | ||
| B、24 | ||
C、10
| ||
D、12
|
查看答案和解析>>
科目:初中数学 来源: 题型:
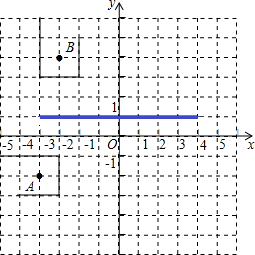 如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍(不包括坐标轴所表示的紫线),试用坐标写出一条机械手在移动中可能要经过的路线(机械手的行走路线均经过格点)
如图,机械手要将一个工件从图中的A处移动到B处,但是这个工件不能碰到图中的障碍(不包括坐标轴所表示的紫线),试用坐标写出一条机械手在移动中可能要经过的路线(机械手的行走路线均经过格点)查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com