练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

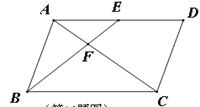
    【题目】如图，在□ABCD中，E是AD的中点，BE交AC于点F，若△AEF的面积为3，则四边形EFCD的面积是_________

    【答案】15

    【解析】

    由四边形ABCD是平行四边形，可证得△AEF∽△CBF，又由点E是AD中点，△AEF的面积为3，即可求得△EFC，△EDC的面积，即可求得答案．

    解：连接EC，

    ∵E是AD的中点，
    ∴AE=ED=AD，
    ∵四边形ABCD是平行四边形，
    ∴AD=BC，AD∥BC，
    ∴△AEF∽△CBF，
    ∴，
    ∴，
    ∵△AEF的面积为3，
    ∴S△EFC=2S△AEF=6，
    ∴S△AEC=9，
    ∵AE=ED，
    ∴S△AEC=S△EDC=9，
    ∴四边形EFCD的面积=S△ACD-S△AEF=18-3=15.
    故答案为：15．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

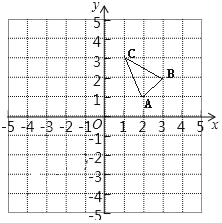
    【题目】在边长为1个单位长度的正方形网格中建立如图所示的平面直角坐标系，△ABC的顶点都在格点上，请解答下列问题：

    （1）作出△ABC向左平移4个单位长度后得到的△A1B1C1，并写出点C1的坐标；

    （2）将△A1B1C1绕原点O逆时针旋转90°得到△A2B2C2，请画出旋转后的△A2B2C2，并写出点C2的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图，航母由西向东航行，到达处时，测得小岛位于它的北偏东方向，且与航母相距80海里，再航行一段时间后到达B处，测得小岛位于它的北偏东方向.如果航母继续航行至小岛的正南方向的处，求还需航行的距离的长.

    （参考数据：，，，，，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在菱形ABCD中，∠BAD＝120°，CE⊥AD，且CE＝BC，连接BE交对角线AC于点F，则∠EFC＝_____°．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

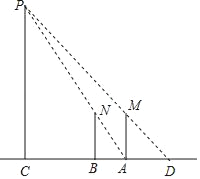
    【题目】甲和乙两位同学想测量一下广场中央的照明灯P的高度，如图，当甲站在A处时，乙测得甲的影子长AD正好与他的身高AM相等，接着甲沿AC方向继续向前走，走到点B处时，甲的影子刚好是线段AB，此时测得AB的长为1.2m．已知甲直立时的身高为1.8m，求照明灯的高CP的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

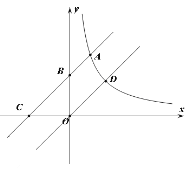
    【题目】直线y=kx与反比例函数y=（x＞0）的图象相交点D(，m),将直线y=kx向上平移b个单位长度与反比例函数的图象交于点A，与y轴交于点B，与x轴交于点C，且,求平移后的直线的表达式.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，BC＞AB＞AC．甲、乙两人想在BC上取一点P，使得∠APC＝2∠ABC，其作法如下：

    （甲）作AB的中垂线，交BC于P点，则P即为所求；

    （乙）以B为圆心，AB长为半径画弧，交BC于P点，则P即为所求．

    对于两人的作法，下列判断何者正确？（　　）

    A. 两人皆正确B. 两人皆错误C. 甲正确，乙错误D. 甲错误，乙正确

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，D为⊙O上一点，点C在直线BA的延长线上，且∠CDA=∠CBD．

    （1）求证：CD是⊙O的切线；

    （2）若BC=8cm，tan∠CDA=，求⊙O的半径；

    （3）在（2）条件下，过点B作⊙O的切线交CD的延长线于点E，连接OE，求四边形OEDA的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

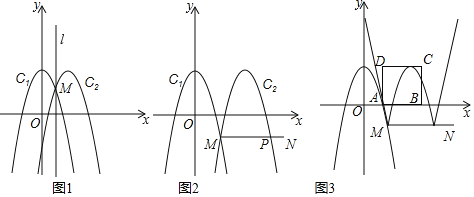
    【题目】定义：如图1，在平面直角坐标系中，点是二次函数图象上一点，过点作轴，如果二次函数的图象与关于成轴对称，则称是关于点的伴随函数．如图2，在平面直角坐标系中，二次函数的函数表达式是，点是二次函数图象上一点，且点的横坐标为，二次函数是关于点的伴随函数．

    （1）若，求的函数表达式．

    （2）过点作轴，如果，线段与的图象交于点，且，求的值．

    （3）如图3，二次函数的图象在上方的部分记为，剩余的部分沿翻折得到，由和所组成的图象记为．以、为顶点在轴上方作正方形．直接写出正方形与有三个公共点时的取值范围．

    查看答案和解析>>

    同步练习册答案