
ΓΨΧβΡΩΓΩΕ®“εΘΚ»γΆΦ1Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Βψ![]() «Εΰ¥ΈΚ· ΐ
«Εΰ¥ΈΚ· ΐ![]() ΆΦœσ…œ“ΜΒψΘ§ΙΐΒψ
ΆΦœσ…œ“ΜΒψΘ§ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§»γΙϊΕΰ¥ΈΚ· ΐ
÷αΘ§»γΙϊΕΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ”κ
ΒΡΆΦœσ”κ![]() ΙΊ”Ύ
ΙΊ”Ύ![]() ≥…÷αΕ‘≥ΤΘ§‘ρ≥Τ
≥…÷αΕ‘≥ΤΘ§‘ρ≥Τ![]() «
«![]() ΙΊ”ΎΒψ
ΙΊ”ΎΒψ![]() ΒΡΑιΥφΚ· ΐΘ°»γΆΦ2Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Εΰ¥ΈΚ· ΐ
ΒΡΑιΥφΚ· ΐΘ°»γΆΦ2Θ§‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒ÷–Θ§Εΰ¥ΈΚ· ΐ![]() ΒΡΚ· ΐ±μ¥ο Ϋ «
ΒΡΚ· ΐ±μ¥ο Ϋ «![]() Θ§Βψ
Θ§Βψ![]() «Εΰ¥ΈΚ· ΐ
«Εΰ¥ΈΚ· ΐ![]() ΆΦœσ…œ“ΜΒψΘ§«“Βψ
ΆΦœσ…œ“ΜΒψΘ§«“Βψ![]() ΒΡΚαΉχ±ξΈΣ
ΒΡΚαΉχ±ξΈΣ![]() Θ§Εΰ¥ΈΚ· ΐ
Θ§Εΰ¥ΈΚ· ΐ![]() «
«![]() ΙΊ”ΎΒψ
ΙΊ”ΎΒψ![]() ΒΡΑιΥφΚ· ΐΘ°
ΒΡΑιΥφΚ· ΐΘ°
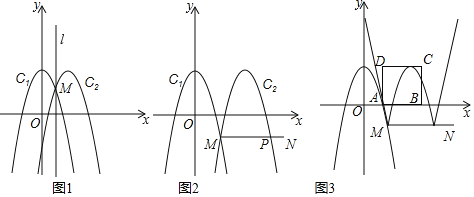
Θ®1Θ©»τ![]() Θ§«σ
Θ§«σ![]() ΒΡΚ· ΐ±μ¥ο ΫΘ°
ΒΡΚ· ΐ±μ¥ο ΫΘ°
Θ®2Θ©ΙΐΒψ![]() Ής
Ής![]() ÷αΘ§»γΙϊ
÷αΘ§»γΙϊ![]() Θ§œΏΕΈ
Θ§œΏΕΈ![]() ”κ
”κ![]() ΒΡΆΦœσΫΜ”ΎΒψ
ΒΡΆΦœσΫΜ”ΎΒψ![]() Θ§«“
Θ§«“![]() Θ§«σ
Θ§«σ![]() ΒΡ÷ΒΘ°
ΒΡ÷ΒΘ°
Θ®3Θ©»γΆΦ3Θ§Εΰ¥ΈΚ· ΐ![]() ΒΡΆΦœσ‘Ύ
ΒΡΆΦœσ‘Ύ![]() …œΖΫΒΡ≤ΩΖ÷Φ«ΈΣ
…œΖΫΒΡ≤ΩΖ÷Φ«ΈΣ![]() Θ§ Θ”ύΒΡ≤ΩΖ÷―Ί
Θ§ Θ”ύΒΡ≤ΩΖ÷―Ί![]() Ζ≠’έΒΟΒΫ
Ζ≠’έΒΟΒΫ![]() Θ§”…
Θ§”…![]() ΚΆ
ΚΆ![]() ΥυΉι≥…ΒΡΆΦœσΦ«ΈΣ
ΥυΉι≥…ΒΡΆΦœσΦ«ΈΣ![]() Θ°“‘
Θ°“‘![]() ΓΔ
ΓΔ![]() ΈΣΕΞΒψ‘Ύ
ΈΣΕΞΒψ‘Ύ![]() ÷α…œΖΫΉς’ΐΖΫ–Έ
÷α…œΖΫΉς’ΐΖΫ–Έ![]() Θ°÷±Ϋ”–¥≥ω’ΐΖΫ–Έ
Θ°÷±Ϋ”–¥≥ω’ΐΖΫ–Έ![]() ”κ
”κ![]() ”–»ΐΗωΙΪΙ≤Βψ ±
”–»ΐΗωΙΪΙ≤Βψ ±![]() ΒΡ»Γ÷ΒΖΕΈßΘ°
ΒΡ»Γ÷ΒΖΕΈßΘ°
ΓΨ¥πΑΗΓΩ(1)![]() ;(2)
;(2) ![]() ;(3)ΦϊΫβΈω.
;(3)ΦϊΫβΈω.
ΓΨΫβΈωΓΩ
Θ®1Θ©Β±![]() ±Θ§≈ΉΈοœΏ
±Θ§≈ΉΈοœΏ![]() ”κ≈ΉΈοœΏ
”κ≈ΉΈοœΏ![]() ΙΊ”Ύ÷±œΏ
ΙΊ”Ύ÷±œΏ![]() Ε‘≥ΤΘ§ΒΟ≥ω≈ΉΈοœΏ
Ε‘≥ΤΘ§ΒΟ≥ω≈ΉΈοœΏ![]() ΒΡΕΞΒψ ±
ΒΡΕΞΒψ ±![]() Θ§Φ¥Ω…«σ≥ω
Θ§Φ¥Ω…«σ≥ω![]() ΒΡΫβΈω ΫΘ§Θ®2Θ©”…
ΒΡΫβΈω ΫΘ§Θ®2Θ©”…![]() ÷αΘ§
÷αΘ§![]() Θ§ΒΟ
Θ§ΒΟ![]() Θ§‘ΌΖ÷
Θ§‘ΌΖ÷![]() ”κ
”κ![]() Ζ÷άύΧ÷¬έΦ¥Ω…;Θ®3Θ©Ζ÷ΈωΆΦœσΩ…÷ΣΘΚΒ±
Ζ÷άύΧ÷¬έΦ¥Ω…;Θ®3Θ©Ζ÷ΈωΆΦœσΩ…÷ΣΘΚΒ±![]() ±Θ§Ω…÷Σ
±Θ§Ω…÷Σ![]() ΚΆ
ΚΆ![]() ΒΡΕ‘≥Τ÷αΙΊ”Ύ÷±œΏ
ΒΡΕ‘≥Τ÷αΙΊ”Ύ÷±œΏ![]() Ε‘≥ΤΘ§
Ε‘≥ΤΘ§![]() ΒΡΕΞΒψ«Γ‘Ύ
ΒΡΕΞΒψ«Γ‘Ύ![]() …œΘ§¥Υ ±
…œΘ§¥Υ ±![]() ”κ’ΐΖΫ–Έ«Γ”…2ΗωΫΜΒψΘ§Ι Ω…ΒΟ≥ωΫα¬έ.
”κ’ΐΖΫ–Έ«Γ”…2ΗωΫΜΒψΘ§Ι Ω…ΒΟ≥ωΫα¬έ.
ΫβΘΚΘ®1Θ©Β±![]() ±Θ§≈ΉΈοœΏ
±Θ§≈ΉΈοœΏ![]() ”κ≈ΉΈοœΏ
”κ≈ΉΈοœΏ![]() ΙΊ”Ύ÷±œΏ
ΙΊ”Ύ÷±œΏ![]() Ε‘≥ΤΘ§
Ε‘≥ΤΘ§
Γύ≈ΉΈοœΏ![]() ΒΡΕΞΒψ ±
ΒΡΕΞΒψ ±![]() Θ§
Θ§
Γύ≈ΉΈοœΏ![]() ΒΡΫβΈω ΫΈΣ
ΒΡΫβΈω ΫΈΣ![]() .
.
Θ®2Θ©ΓΏ![]() ÷αΘ§
÷αΘ§![]() Θ§
Θ§
Γύ![]() .
.
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
![]() .
.
Β±![]() ±Θ§
±Θ§![]() Θ§
Θ§
![]() .
.
Θ®3Θ©Ζ÷ΈωΆΦœσΩ…÷ΣΘΚΒ±![]() ±Θ§Ω…÷Σ
±Θ§Ω…÷Σ![]() ΚΆ
ΚΆ![]() ΒΡΕ‘≥Τ÷αΙΊ”Ύ÷±œΏ
ΒΡΕ‘≥Τ÷αΙΊ”Ύ÷±œΏ![]() Ε‘≥ΤΘ§
Ε‘≥ΤΘ§![]() ΒΡΕΞΒψ«Γ‘Ύ
ΒΡΕΞΒψ«Γ‘Ύ![]() …œΘ§¥Υ ±
…œΘ§¥Υ ±![]() ”κ’ΐΖΫ–Έ«Γ”…2ΗωΫΜΒψΘ°
”κ’ΐΖΫ–Έ«Γ”…2ΗωΫΜΒψΘ°
Β±![]() ±Θ§÷±œΏ
±Θ§÷±œΏ![]() ”κ
”κ![]() ÷α÷ΊΚœΘ§
÷α÷ΊΚœΘ§![]() ”κ’ΐΖΫ–Έ«Γ”…»ΐΗωΕΞΒψΘ°
”κ’ΐΖΫ–Έ«Γ”…»ΐΗωΕΞΒψΘ°
Β±![]() ±Θ§
±Θ§![]() ΙΐΒψ
ΙΐΒψ![]() «“
«“![]() Ε‘≥Τ÷αΉσ≤ύ≤ΩΖ÷”κ’ΐΖΫ–Έ”–ΝΫΗωΫΜΒψ
Ε‘≥Τ÷αΉσ≤ύ≤ΩΖ÷”κ’ΐΖΫ–Έ”–ΝΫΗωΫΜΒψ
Β±![]() Μρ
Μρ![]() ±Θ§
±Θ§![]() ”κ’ΐΖΫ–Έ
”κ’ΐΖΫ–Έ![]() ”–»ΐΗωΙΪΙ≤ΒψΘ°
”–»ΐΗωΙΪΙ≤ΒψΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
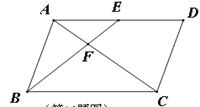
ΓΨΧβΡΩΓΩ»γΆΦΘ§‘ΎΓθABCD÷–Θ§E «ADΒΡ÷–ΒψΘ§BEΫΜAC”ΎΒψFΘ§»τΓςAEFΒΡΟφΜΐΈΣ3Θ§‘ρΥΡ±Ώ–ΈEFCDΒΡΟφΜΐ «_________
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§AB «![]() ΒΡ÷±ΨΕΘ§ΒψD «ΑκΨΕOAΒΡ÷–ΒψΘ§ΙΐΒψDΉςCDΓΆABΘ§ΫΜ
ΒΡ÷±ΨΕΘ§ΒψD «ΑκΨΕOAΒΡ÷–ΒψΘ§ΙΐΒψDΉςCDΓΆABΘ§ΫΜ![]() ”ΎΒψCΘ§ΒψEΈΣΜΓBCΒΡ÷–ΒψΘ§Ν§ΫαED≤Δ―”≥ΛEDΫΜ
”ΎΒψCΘ§ΒψEΈΣΜΓBCΒΡ÷–ΒψΘ§Ν§ΫαED≤Δ―”≥ΛEDΫΜ![]() ”ΎΒψFΘ§Ν§ΫαAFΓΔBFΘ§‘ρΘ® Θ©
”ΎΒψFΘ§Ν§ΫαAFΓΔBFΘ§‘ρΘ® Θ©
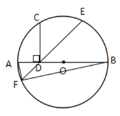
A. sinΓœAFE=![]() B. cosΓœBFE=
B. cosΓœBFE=![]() C. tanΓœEDB=
C. tanΓœEDB=![]() D. tanΓœBAF=
D. tanΓœBAF=![]()
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ“―÷Σ:ΒψP «’ΐΖΫ–ΈΡΎ“ΜΒψ,ΓςABP–ΐΉΣΚσΡή”κΓςCBE÷ΊΚœ.

(1)ΓςABP–ΐΉΣΒΡ–ΐΉΣ÷––Ρ « ≤Ο¥?–ΐΉΣΝΥΕύ…ΌΕ»?
(2)»τBP=2,«σPEΒΡ≥Λ.
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§![]() «
«![]() ΒΡ÷±ΨΕΘ§
ΒΡ÷±ΨΕΘ§![]() «
«![]() …œ“ΜΒψΘ§
…œ“ΜΒψΘ§![]() ‘Ύ
‘Ύ![]() ΒΡ―”≥ΛœΏ…œΘ§«“
ΒΡ―”≥ΛœΏ…œΘ§«“![]() Θ°
Θ°
Θ®1Θ©«σ÷ΛΘΚ![]() «
«![]() ΒΡ«–œΏΘΜ
ΒΡ«–œΏΘΜ
Θ®2Θ©![]() ΒΡΑκΨΕΈΣ
ΒΡΑκΨΕΈΣ![]() Θ§
Θ§![]() Θ§«σ
Θ§«σ![]() ΒΡ≥ΛΘ°
ΒΡ≥ΛΘ°

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩΒψAΓΔCΈΣΑκΨΕ «3ΒΡ‘≤÷ή…œΝΫΒψΘ§ΒψBΈΣΜΓACΒΡ÷–ΒψΘ§“‘œΏΕΈBAΓΔBCΈΣΝΎ±ΏΉςΝβ–ΈABCDΘ§ΕΞΒψD«Γ‘ΎΗΟ‘≤÷±ΨΕΒΡ»ΐΒ»Ζ÷Βψ…œΘ§‘ρΗΟΝβ–ΈΒΡ±Ώ≥ΛΈΣ_____Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ»γΆΦΘ§“―÷Σ≈ΉΈοœΏΨ≠Ιΐ‘≠ΒψOΘ§ΕΞΒψΈΣAΘ®1Θ§1Θ©Θ§«“”κ÷±œΏy=x©¹2ΫΜ”ΎBΘ§CΝΫΒψΘ°
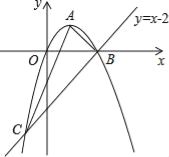
Θ®1Θ©«σ≈ΉΈοœΏΒΡΫβΈω ΫΦΑΒψCΒΡΉχ±ξΘΜ
Θ®2Θ©«σ÷ΛΘΚΓςABC «÷±Ϋ«»ΐΫ«–ΈΘΜ
Θ®3Θ©»τΒψNΈΣx÷α…œΒΡ“ΜΗωΕ·ΒψΘ§ΙΐΒψNΉςMNΓΆx÷α”κ≈ΉΈοœΏΫΜ”ΎΒψMΘ§‘ρ «Ζώ¥φ‘Ύ“‘OΘ§MΘ§NΈΣΕΞΒψΒΡ»ΐΫ«–Έ”κΓςABCœύΥΤΘΩ»τ¥φ‘ΎΘ§«κ«σ≥ωΒψNΒΡΉχ±ξΘΜ»τ≤Μ¥φ‘ΎΘ§«κΥΒΟςάμ”…Θ°
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ«ύΡξ¬Ο––…γΈΣΈϋ“ΐ”ΈΩΆΉιΆ≈»ΞΓΑΜΤΙϊ ς--ΝζΙ§--÷·ΫπΕ¥Γ±“ΜœΏ¬Ο”ΈΘ§ΆΤ≥ωΝΥ»γœ¬ ’Ζ―±ξΉΦ![]() »γΆΦΥυ Ψ
»γΆΦΥυ Ψ![]() ΘΚΡ≥ΒΞΈΜΉι÷·‘±ΙΛ»ΞΓΑΜΤΙϊ ς--ΝζΙ§--÷·ΫπΕ¥Γ±“ΜœΏ¬Ο”ΈΘ§Ι≤÷ßΗΕΗχ¬Ο––…γ¬Ο”ΈΖ―”Ο27000‘ΣΘ§«κΈ ΗΟΒΞΈΜ’β¥ΈΙ≤”–Εύ…ΌΟϊ‘±ΙΛ»ΞΓΑΜΤΙϊ ς--ΝζΙ§--÷·ΫπΕ¥Γ±“ΜœΏ¬Ο”ΈΘΩ
ΘΚΡ≥ΒΞΈΜΉι÷·‘±ΙΛ»ΞΓΑΜΤΙϊ ς--ΝζΙ§--÷·ΫπΕ¥Γ±“ΜœΏ¬Ο”ΈΘ§Ι≤÷ßΗΕΗχ¬Ο––…γ¬Ο”ΈΖ―”Ο27000‘ΣΘ§«κΈ ΗΟΒΞΈΜ’β¥ΈΙ≤”–Εύ…ΌΟϊ‘±ΙΛ»ΞΓΑΜΤΙϊ ς--ΝζΙ§--÷·ΫπΕ¥Γ±“ΜœΏ¬Ο”ΈΘΩ

≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ
ΓΨΧβΡΩΓΩ‘ΎΤΫΟφ÷±Ϋ«Ήχ±ξœΒxOy÷–Θ§≈ΉΈοœΏ![]() Ψ≠ΙΐΒψ
Ψ≠ΙΐΒψ![]() Θ§
Θ§![]() Θ°
Θ°
![]() «σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΦΑΕ‘≥Τ÷αΘΜ
«σΗΟ≈ΉΈοœΏΒΡΚ· ΐ±μ¥ο ΫΦΑΕ‘≥Τ÷αΘΜ
![]() …ηΒψBΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣCΘ§ΒψD «≈ΉΈοœΏΕ‘≥Τ÷α…œ“ΜΕ·ΒψΘ§Φ«≈ΉΈοœΏ‘ΎAΘ§B÷°ΦδΒΡ≤ΩΖ÷ΈΣΆΦœσ
…ηΒψBΙΊ”Ύ‘≠ΒψΒΡΕ‘≥ΤΒψΈΣCΘ§ΒψD «≈ΉΈοœΏΕ‘≥Τ÷α…œ“ΜΕ·ΒψΘ§Φ«≈ΉΈοœΏ‘ΎAΘ§B÷°ΦδΒΡ≤ΩΖ÷ΈΣΆΦœσ![]() ΑϋΚ§AΘ§BΝΫΒψ
ΑϋΚ§AΘ§BΝΫΒψ![]() Θ§»γΙϊ÷±œΏCD”κΆΦœσG”–ΝΫΗωΙΪΙ≤ΒψΘ§ΫαΚœΚ· ΐΒΡΆΦœσΘ§÷±Ϋ”–¥≥ωΒψDΉίΉχ±ξtΒΡ»Γ÷ΒΖΕΈßΘ°
Θ§»γΙϊ÷±œΏCD”κΆΦœσG”–ΝΫΗωΙΪΙ≤ΒψΘ§ΫαΚœΚ· ΐΒΡΆΦœσΘ§÷±Ϋ”–¥≥ωΒψDΉίΉχ±ξtΒΡ»Γ÷ΒΖΕΈßΘ°
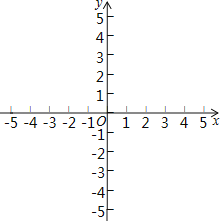
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΙζΦ ―ß–Θ”≈―Γ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com