
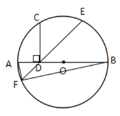
【题目】如图,AB是![]() 的直径,点D是半径OA的中点,过点D作CD⊥AB,交
的直径,点D是半径OA的中点,过点D作CD⊥AB,交![]() 于点C,点E为弧BC的中点,连结ED并延长ED交
于点C,点E为弧BC的中点,连结ED并延长ED交![]() 于点F,连结AF、BF,则( )
于点F,连结AF、BF,则( )
A. sin∠AFE=![]() B. cos∠BFE=
B. cos∠BFE=![]() C. tan∠EDB=
C. tan∠EDB=![]() D. tan∠BAF=
D. tan∠BAF=![]()
【答案】C
【解析】
连接OC,OE,过E作EH⊥AB于H,根据OC=2OD可得∠COD=60°,则∠BOC=120°,由E为弧BC的中点,得∠BOE=60°,则∠BFE=30°,进而可得∠AFE=90°﹣∠BFE=60°,再求出对应的三角形函数值,然后根据CD=![]() OD,可得
OD,可得![]() 的值,进而到tan∠EDB的值
的值,进而到tan∠EDB的值
解:如图,连接OC,OE,过E作EH⊥AB于H,
∵点D是半径OA的中点,CD⊥AB,
∴∠COD=60°,即∠BOC=120°,
∴CD=![]() OD,
OD,
∵E为弧BC的中点,
∴∠BOE=60°,EH=CD,H为半径OB的中点,
∴∠BFE=30°,则cos∠BFE=![]() ;
;
又∵AB为直径,
∴∠AFB=90°,
∴∠AFE=90°﹣∠BFE=60°,则sin∠AFE=![]() ;
;
∵EH=CD,
∴tan∠EDB=![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】由我国完全自主设计、自主建造的首艘国产航母于2018年5月成功完成第一次海上试验任务.如图,航母由西向东航行,到达![]() 处时,测得小岛
处时,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛
方向,且与航母相距80海里,再航行一段时间后到达B处,测得小岛![]() 位于它的北偏东
位于它的北偏东![]() 方向.如果航母继续航行至小岛
方向.如果航母继续航行至小岛![]() 的正南方向的
的正南方向的![]() 处,求还需航行的距离
处,求还需航行的距离![]() 的长.
的长.
(参考数据:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,BC>AB>AC.甲、乙两人想在BC上取一点P,使得∠APC=2∠ABC,其作法如下:
(甲)作AB的中垂线,交BC于P点,则P即为所求;
(乙)以B为圆心,AB长为半径画弧,交BC于P点,则P即为所求.
对于两人的作法,下列判断何者正确?( )
![]()
A. 两人皆正确B. 两人皆错误C. 甲正确,乙错误D. 甲错误,乙正确
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,D为⊙O上一点,点C在直线BA的延长线上,且∠CDA=∠CBD.

(1)求证:CD是⊙O的切线;
(2)若BC=8cm,tan∠CDA=![]() ,求⊙O的半径;
,求⊙O的半径;
(3)在(2)条件下,过点B作⊙O的切线交CD的延长线于点E,连接OE,求四边形OEDA的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,CD是⊙O的一条弦,且CD⊥AB于点E,连接AD,BC,CO
(1)当∠BCO=25°时,求∠A的度数;
(2)若CD=4![]() ,BE=4,求⊙O的半径.
,BE=4,求⊙O的半径.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了满足学生的个性化需求,新课程改革已经势在必行,某校积极开展拓展性课程建设,大体分为学科、文体、德育、其他等四个框架进行拓展课程设计。为了了解学生喜欢的拓展课程类型,学校随机抽取了部分学生进行调查,调查后将数据绘制成扇形统计图和条形统计图(未绘制完整).

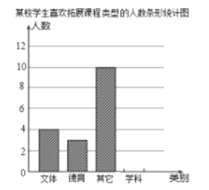
(1)求调查的学生总人数,并把条形图补充完整并填写扇形图中缺失的数据;
(2)小明同学说:“因为调查的同学中喜欢文体类拓展课程的同学占16%,而喜欢德育类拓展课程的同学仅占12%,所以全校2000名学生中,喜欢文体类拓展课程的同学人数一定比喜欢德育类拓展课程的同学人数多。”你觉得小明说得对吗?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A、D、C、F在同一条直线上,AD=CF,AB=DE,BC=EF.
(1)求证:ΔABC≌△DEF;
(2)若∠A=55°,∠B=88°,求∠F的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:如图1,在平面直角坐标系中,点![]() 是二次函数
是二次函数![]() 图象上一点,过点
图象上一点,过点![]() 作
作![]() 轴,如果二次函数
轴,如果二次函数![]() 的图象与
的图象与![]() 关于
关于![]() 成轴对称,则称
成轴对称,则称![]() 是
是![]() 关于点
关于点![]() 的伴随函数.如图2,在平面直角坐标系中,二次函数
的伴随函数.如图2,在平面直角坐标系中,二次函数![]() 的函数表达式是
的函数表达式是![]() ,点
,点![]() 是二次函数
是二次函数![]() 图象上一点,且点
图象上一点,且点![]() 的横坐标为
的横坐标为![]() ,二次函数
,二次函数![]() 是
是![]() 关于点
关于点![]() 的伴随函数.
的伴随函数.
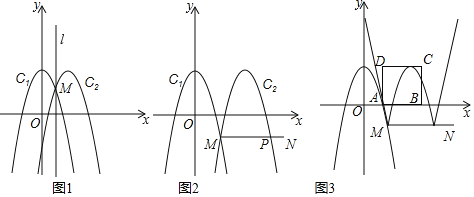
(1)若![]() ,求
,求![]() 的函数表达式.
的函数表达式.
(2)过点![]() 作
作![]() 轴,如果
轴,如果![]() ,线段
,线段![]() 与
与![]() 的图象交于点
的图象交于点![]() ,且
,且![]() ,求
,求![]() 的值.
的值.
(3)如图3,二次函数![]() 的图象在
的图象在![]() 上方的部分记为
上方的部分记为![]() ,剩余的部分沿
,剩余的部分沿![]() 翻折得到
翻折得到![]() ,由
,由![]() 和
和![]() 所组成的图象记为
所组成的图象记为![]() .以
.以![]() 、
、![]() 为顶点在
为顶点在![]() 轴上方作正方形
轴上方作正方形![]() .直接写出正方形
.直接写出正方形![]() 与
与![]() 有三个公共点时
有三个公共点时![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我市智慧阅读活动正如火如茶地进行.某班学习委员为了解11月份全班同学课外阅读的情况,调查了全班同学11月份读书的册数,并根据调查结果绘制了如下不完整的条形统计图和扇形统计图:
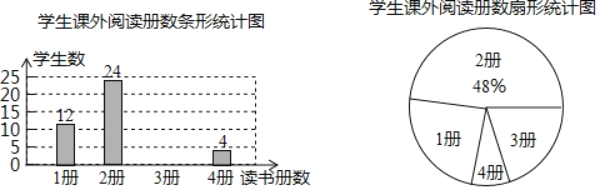
(1)扇形统计图中“3册”部分所对应的圆心角的度数是 ,并把条形统计图补充完整;
(2)该班的学习委员11月份的读书册数为4册,若该班的班主任从11月份读书4册的学生中随机抽取两名同学参加学校举行的知识竞赛,请用列表法或画树状图求恰好有一名同学是学习委员的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com