
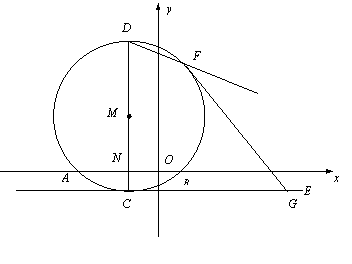
如图,⊙M与x轴交于A、B两点,其坐标分别为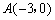 、
、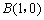 ,直径CD⊥x轴于N
,直径CD⊥x轴于N ,抛物线
,抛物线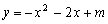 经过A、B、D三点,
经过A、B、D三点,
(1) 求m的值及点D的坐标.
(2)若直线CE切⊙M于点C,G在直线CE上,已知点G的横坐标为3. 求G的纵坐标
(3) 对于(2)中的G,是否存在过点G的直线,使它与(1)中抛物线只有一个交点,请说明理由.
(4) 对于(2)中的G 直线FG切⊙M于点F,求直线DF的解析式.
解 (1) ∵抛物线过A、B两点,
代入得 m=3. -------------2分
∴抛物线为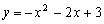 .
.
又抛物线过点D,由圆的对称性知点D为抛物线的顶点.
∴D点坐标为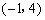 . -------------4分
. -------------4分
(2) 设 NC= a,则 DC=4+ a,半径=2+ a/2,MN=2-a/2
∵CD⊥x轴,∴NA=NB=2. ∴ON=1.
在直角三角形AMN中,(2+ a/2)2=4+(2-a/2)2 -------------6分
∴a=1.∴NC=1. G的纵坐标为-1 -------------7分
(3) 假设存在过点G的直线为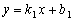 ,
,
则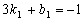 ,∴
,∴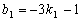 . -------------8分
. -------------8分
由方程组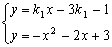 得
得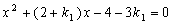 -------------9分
-------------9分
∵交点只有一个,∴(2+k1)2﹣4(﹣4﹣3 k1)=0
k12+16 k1+20=0
∵162﹣80>0
∴k1存在,∴这样的直线存在-------------10分
(4)设直线DF交CE于P,连结CF,则∠CFP=90°.
∴∠2+∠3=∠1+∠4=90°.
∵GC、GF是切线,
 ∴GC=GF. ∴∠3=∠4.
∴GC=GF. ∴∠3=∠4.
∴∠1=∠2.
∴GF=GP.
∴GC=GP.
可得CP=8. -------------12分
∴P点坐标为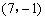 -------------13分
-------------13分
设直线DF的解析式为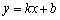
则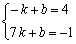 解得
解得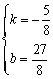
∴直线DF的解析式为: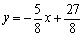


科目:初中数学 来源: 题型:
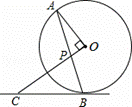
如图,AB是⊙O的弦,OP⊥OA交AB于点P,过点B的直线交OP的延长线于点C,且CP=CB.
(1)求证:BC是⊙O的切线;
(2)若⊙O的半径为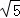 ,OP=1.求BC的长.
,OP=1.求BC的长.
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
某商店经营一种成本为每千克40美元的水产品,根据市场分析,若按每千克50元销售,一个月能售出500千克;销售价每涨1元,月销售量就减少10千克,
(1)针对这种水产品的销售情况,设销售单价定为x元(x>50),
请用的x代数式表示月销售量, 以及获得 的利润.
的利润.
(2)当x取什么数时利润最大? 最大利润是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
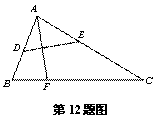
如图,有一张△ABC纸片,AC=8,∠C=30°,点E在AC边上,点D在边AB上,沿着DE对折,使点A落在BC边上的点F处,则CE的最大值为( )
A.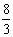 B.
B.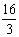 C.4 D.
C.4 D.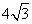
 |
查看答案和解析>>
科目:初中数学 来源: 题型:
“神舟五号”载人飞船绕地球飞行了14圈,共飞行约590200km,则这个飞行距离用科学记数法表示为 ( )
A 59.02×104 km B 0.5902×106 km C 5.902×104 km D 5.902 ×105 km
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com