
分析 ①把2根据规定运算写成1+1代入即可得出结论正确;
②由于a>b,设a=b+n(n为整数)代入规定化简即可得出结论正确;
③根据规定f(a-b)+f(a+b)=0,再判断出f(a)≥$\sqrt{2}$,即可得出结论不正确;
④将f(a-b)•f(a+b)根据规定化简得出右边,即可判断出结论正确.
解答 解:①f(2)=f(1+1)=f(1)•f(1)=$\sqrt{2}×\sqrt{2}$=2,
∴①正确;
②设a=b+n,n为正整数,
∴f(a)=f(b)+f(n)=f(b)+nf(1)=f(b)+$\sqrt{2}$n>f(b),
∴②正确;
③∵f(a-b)+f(a+b)=-f(a)•f(b)+f(a)•f(b)=0,
由②知f(a)≥f(1),
∵f(1)=$\sqrt{2}$,
∴f(a)≥$\sqrt{2}$≠0,
∴③不正确;
④∵f(a-b)•f(a+b)=f(a-b+a+b)=f(2a),
∴④正确;
∴正确的有①②④
故答案为①②④.
点评 此题是实数运算,主要考查了学生的理解规定和运用规定的能力,是一道简单的新定义题目.


科目:初中数学 来源: 题型:填空题
 如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.
如图,矩形ABCD的两个顶点A、B分别落在x、y轴上,顶点C、D位于第一象限,且OA=3,OB=2,对角线AC、BD交于点G,若曲线y=$\frac{k}{x}$(x>0)经过点C、G,则k=$\frac{7}{2}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
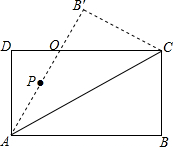 如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.
如图,在矩形ABCD中,∠CAB=30°,BC=4$\sqrt{3}$cm,将△ABC沿AC边翻折,使点B到点B′,AB′与DC相交于点O.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A.
已知:如图,在△ABC中,∠A=∠ABC,直线EF分别交△ABC的边AB、AC和CB的延长线于点D、E、F.求证:∠F+∠FEC=2∠A.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )
如图,四边形PAOB是扇形OMN的内接矩形,顶点P在$\widehat{MN}$上,且不与M、N重合,当P点在$\widehat{MN}$上移动时,矩形PAOB的形状,大小随之变化,则AB的长度( )| A. | 不变 | B. | 变小 | C. | 变大 | D. | 不能确定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com