
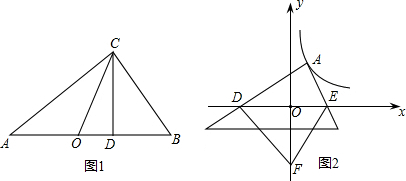
分析 (1)根据题中的例子即可直接得出结论;
(2)根据直角三角形的性质得出CO=a+b,CD=$\sqrt{ab}$,再由(1)中的结论即可得出等号成立时的条件;
(3)过点A作AH⊥x轴于点H,根据S四边形ADFE=S△ADE+S△FDE可知当DH=EH时DE最小,由此可得出结论.
解答 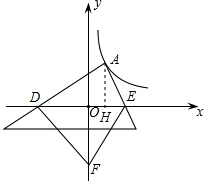 解:(1)∵a+b≥2$\sqrt{ab}$,a、b均为正实数,
解:(1)∵a+b≥2$\sqrt{ab}$,a、b均为正实数,
∴当且仅当a、b满足a=b时,a+b有最小值.
故答案为:a=b;
(2)∵△ABC中,∠ACB=90°,CD⊥AB,CO为AB边上中线,AD=2a,DB=2b,
∴OC=$\frac{1}{2}$(AD+BD)=a+b,CD=2$\sqrt{ab}$,OC≥CD,即a+b≥2$\sqrt{ab}$,
∴当点D与点O重合时等式成立;
(3)如图所示,过点A作AH⊥x轴于点H,
∵S四边形ADFE=S△ADE+S△FDE=$\frac{1}{2}$DE•|yA|+$\frac{1}{2}$DE•OF=$\frac{1}{2}$DE(|yA|+OF),
∴当DH=EH时DE最小,
∴A点的横坐标为1,
∴AH=4,
∴DE最小为8,
∴S四边形ADFE=$\frac{1}{2}$×8×(4+3)=28.
点评 本题考查的是反比例函数综合题,涉及到用配方法可求最大(小)值,在a+b≥2$\sqrt{ab}$(a、b均为正实数)中,若ab为定值,则当且仅当a、b满足a=b时,a+b有最小值2$\sqrt{ab}$是解答此题的关键.


科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
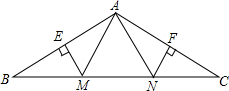 如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )
如图所示,在等腰△ABC中,∠BAC=120°,若EM和FN分别垂直平分AB和AC,垂足分别为E、F、M、N都在BC边上,且EM=FN=4,则BC的长度为( )| A. | 12 | B. | 16 | C. | 20 | D. | 24 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
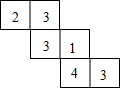 一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.
一个几何体由若干个大小相同的小立方块搭成,从上面看到的这个几何体的形状如图所示.其中小正方形中的数字表示在该位置小立方块的个数,请你画出从正面和从左面看到的这个几何体的形状图.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.
一辆火车从百货大楼出发负责送货,向东走了4千米到达小明家,继续向东走了1.5千米到达小红家,然后向西走了8.5千米到达小刚家,最后返回百货大楼.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com