
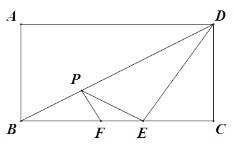
【题目】如图,已知:在矩形ABCD中,AB=2,BC=4,P是对角线BD上的一个动点,作PF⊥BD于P,交边BC于点F(点F与点B、C都不重合),E是射线FC上一动点,连接PE、ED,并一直保持∠EPF=∠FBP,设B、P两点的距离为x,△DEP的面积为y
(1)求出tan∠PBF;
(2)求y关于x的函数解析式,并写出自变量的取值范围
(3)当△DEP与△BCD相似时,求△DEP的面积
【答案】(1)![]() ;(2)
;(2)![]() ;(3)当∠DEP=90°时,面积为
;(3)当∠DEP=90°时,面积为![]() ;当∠PDE=90°时,面积为
;当∠PDE=90°时,面积为![]()
【解析】
(1)利用矩形的性质以及锐角三角函数关系进而得出![]() ,即可得出tan∠PBF的值;
,即可得出tan∠PBF的值;
(2)首先根据相似三角形的判定定理得出![]() ,然后利用相似三角形的性质进而得出
,然后利用相似三角形的性质进而得出![]() ,即可求出y与x的函数关系;
,即可求出y与x的函数关系;
(3)利用当△DEP与△BCD相似时,只有两种情况:∠DEP=∠C=90°或∠EDP=∠C=90°,分别利用勾股定理和相似三角形的性质计算得出答案即可.
(1)∵四边形ABCD是矩形,
![]()
![]()
又![]()
![]()
![]() 即
即![]()
又![]()
![]()
![]()
![]() ,即
,即![]()

如图,作![]() 垂足为H,则
垂足为H,则![]()
又![]()
![]()
![]()
设![]() 则
则![]() ,
,
![]() ,
,
又![]()
由勾股定理得:
![]()
![]() =
=![]()
![]()
又![]()
![]()
当△DEP与△BCD相似时,
只有两种情况:∠DEP=∠C=90°或∠EDP=∠C=90°
①当∠DEP=90°,
∵∠DPE+∠PDE=90°即
∠PDE=∠CBD
∴BE=DE
设CE=a,则BE=DE=4-a
在Rt△DEC中,勾股定理得
![]()
解之![]()
则![]() ,
,
又∵△BCD的面积![]() =4
=4

![]()
②当∠EDP=90°,如图2,
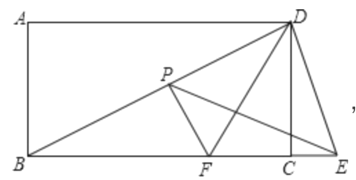
![]()
![]()
![]()
![]()

![]()


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
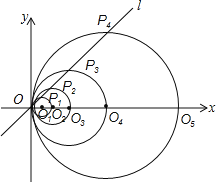
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
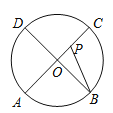
【题目】如图:点A、B、C、D为⊙O上的四等分点,动点P从圆心O出发,沿O﹣C﹣D﹣O的路线做匀速运动.设运动的时间为t秒,∠APB的度数为y.则下列图象中表示y与t之间函数关系最恰当的是( )
A. 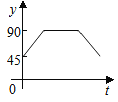 B.
B. 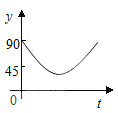 C.
C. 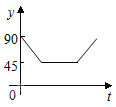 D.
D. 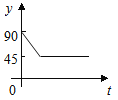
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】老王面前有两个容积相同的杯子,杯子甲他装了三分之一的葡萄酒,杯子乙他装了半杯的王老吉凉茶,老张过来将装有凉茶的杯子乙倒满了酒,老王又将杯子乙中饮料倒一部分到杯子甲,使得两个杯子的饮料分量相同.然后老王让老张先选一杯一起喝了,如果老张不想多喝酒,那么他应该选择( )
A.甲杯B.乙杯C.甲、乙是一样的D.无法确定
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
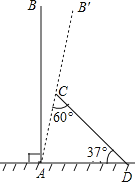
【题目】某次台风来袭时,一棵笔直大树树干AB(假定树干AB垂直于水平地面)被刮倾斜7°(即∠BAB′=7°)后折断倒在地上,树的顶部恰好接触到地面D处,测得∠CDA=37°,AD=5米,求这棵大树AB的高度.(结果保留根号)(参考数据:sin37≈0.6,cos37=0.8,tan37≈0.75)
查看答案和解析>>
科目:初中数学 来源: 题型:
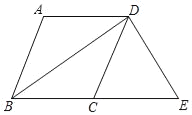
【题目】如图,在四边形ABCD中,AD∥BC,BA=BC,BD平分∠ABC.
(1)求证:四边形ABCD是菱形;
(2)过点D作DE⊥BD,交BC的延长线于点E,若BC=5,BD=8,求四边形ABED的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com