
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 的顶点为P,且与y轴交于点A,与直线
的顶点为P,且与y轴交于点A,与直线![]() 交于点B,C(点B在点C的左侧).
交于点B,C(点B在点C的左侧).
(1)求抛物线![]() 的顶点P的坐标(用含a的代数式表示);
的顶点P的坐标(用含a的代数式表示);
(2)横、纵坐标都是整数的点叫做整点,记抛物线与线段AC围成的封闭区域(不含边界)为“W区域”.
①当![]() 时,请直接写出“W区域”内的整点个数;
时,请直接写出“W区域”内的整点个数;
②当“W区域”内恰有2个整点时,结合函数图象,直接写出a的取值范围.
【答案】(1)顶点P的坐标为![]() ;(2)① 6个;②
;(2)① 6个;② ![]() ,
,![]() .
.
【解析】
(1)由抛物线解析式直接可求;
(2)①由已知可知A(0,2),C(2+![]() ,-2),画出函数图象,观察图象可得;
,-2),画出函数图象,观察图象可得;
②分两种情况求:当a>0时,抛物线定点经过(2,-2)时,a=1,抛物线定点经过(2,-1)时,a=![]() ,则
,则![]() <a≤1;当a<0时,抛物线定点经过(2,2)时,a=-1,抛物线定点经过(2,1)时,a=-
<a≤1;当a<0时,抛物线定点经过(2,2)时,a=-1,抛物线定点经过(2,1)时,a=-![]() ,则-1≤a<-
,则-1≤a<-![]() .
.
解:(1)∵y=ax2-4ax+2a=a(x-2)2-2a,
∴顶点为(2,-2a);
(2)如图,①∵a=2,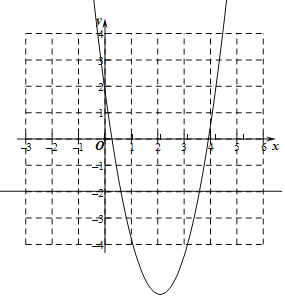
∴y=2x2-8x+2,y=-2,
∴A(0,2),C(2+![]() ,-2),
,-2),
∴有6个整数点;
②当a>0时,抛物线定点经过(2,-2)时,a=1,
抛物线定点经过(2,-1)时,,![]() ;
;
∴ ![]() .
.
当![]() 时,抛物线顶点经过点(2,2)时,
时,抛物线顶点经过点(2,2)时,![]() ;
;
抛物线顶点经过点(2,1)时,![]() ;
;
∴ ![]() .
.
∴综上所述:![]() ,
,![]() .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:初中数学 来源: 题型:
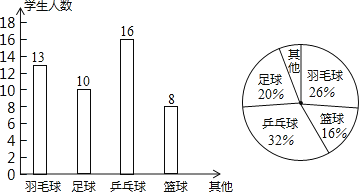
【题目】某校为了组织一次球类对抗赛,在本校随机抽取了若干名学生,对他们每个人最喜欢的一项球类运动进行了统计,将调查结果整理后绘制成如图所示的不完整的统计图,请你依据以上的信息回答下列问题:
(1)求本次被调查的学生人数;
(2)通过计算补全条形统计图;
(3)若全校有4000名学生,请你估计该校最喜欢篮球和足球运动的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
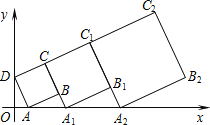
【题目】在平面直角坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2019个正方形的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
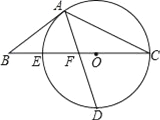
【题目】如图,以△ABC的BC边上一点O为圆心,经过A,C两点且与BC边交于点E,点D为CE的下半圆弧的中点,连接AD交线段EO于点F,若AB=BF.
(1)求证:AB是⊙O的切线;
(2)若CF=4,DF=![]() ,求⊙O的半径r及sinB.
,求⊙O的半径r及sinB.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,半径OC⊥AB于O,AD平分∠CAB交![]() 于点D,连接CD,OD,BD.下列结论中正确的是( )
于点D,连接CD,OD,BD.下列结论中正确的是( )

A.AC∥ODB.![]()
C.△ODE∽△ADOD.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系xOy中,点A(![]() ,3),B(
,3),B(![]() ,2),C(0,
,2),C(0,![]() ).
).
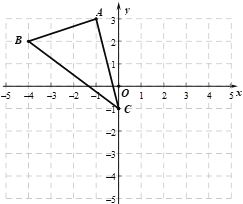
(1)以y轴为对称轴,把△ABC沿y轴翻折,画出翻折后的△![]() ;
;
(2)在(1)的基础上,
①以点C为旋转中心,把△![]() 顺时针旋转90°,画出旋转后的△
顺时针旋转90°,画出旋转后的△![]() ;
;
②点![]() 的坐标为 ,在旋转过程中点
的坐标为 ,在旋转过程中点![]() 经过的路径
经过的路径![]() 的长度为_____(结果保留π).
的长度为_____(结果保留π).
查看答案和解析>>
科目:初中数学 来源: 题型:
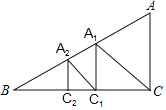
【题目】如图,已知直角△ABC中,AC=6,BC=8,过直角顶点C作CA1⊥AB,垂足为A1,再过A作A1C1⊥BC,垂足为C1,过C1作C1A2⊥AB,垂足为A2,再过A2作A2C2⊥BC,垂足为C2,……,则![]() =_____(其中n为正整数).
=_____(其中n为正整数).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为5的正方形ABCD中,点E在BC边上,连接AE,过D作DF//AE交BC的延长线于点F,过点C作CG⊥DF于点G,延长AE、GC交于点H,点P是线段DG上的任意一点(不与点D、点G重合),连接CP,将△CPG沿CP翻折得到![]() ,连接
,连接![]() . 若CH=1,则
. 若CH=1,则![]() 长度的最小值为__________.
长度的最小值为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() 的图象和
的图象和![]() 轴交于点
轴交于点![]() 、
、![]() ,与
,与![]() 轴交于点
轴交于点![]() ,点
,点![]() 是直线
是直线![]() 上方的抛物线上的动点.
上方的抛物线上的动点.
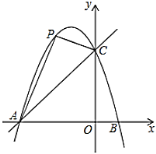
(1)求直线![]() 的解析式.
的解析式.
(2)当![]() 是抛物线顶点时,求
是抛物线顶点时,求![]() 面积.
面积.
(3)在![]() 点运动过程中,求
点运动过程中,求![]() 面积的最大值.
面积的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com