
【题目】如图,直线l1∥l2∥l3,一等腰直角三角形ABC的三个顶点A、B、C分别在l1、l2、l3上,AC交l2于D,∠ACB=90°.已知l1与l2的距离为2,l2与l3的距离为6,则![]() 的值为_____.
的值为_____.

科目:初中数学 来源: 题型:
【题目】如图,有一块矩形纸板,长为20cm,宽为14cm,在它的四角各切去一个同样的正方形,然后将四周突出部分沿虚线折起,就能制作一个无盖的长方体盒子,如果这个无盖的长方体底面积为160cm2,那么该长方体盒子体积是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,∠C=90°,AC=20cm,BC=15cm.现有动点P从点A出发,沿AC向点C方向运动,动点Q从点C出发,沿线段CB也向点B方向运动.如果点P的速度是4cm/秒,点Q的速度是2cm/秒,它们同时出发,当有一点到达所在线段的端点时,就停止运动,设运动的时间为t秒.求:

(1)用含t的代数式表示Rt△CPQ的面积S;
(2)当t=3秒时,P、Q两点之间的距离是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】材料:在学习绝对值时,老师教过我们绝对值的几何含义,![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 、
、![]() 在数轴上对应的两点之间的距离;
在数轴上对应的两点之间的距离;![]() ,所以
,所以![]() 表示
表示![]() 在数轴上对应的点到原点的距离,一般地,点
在数轴上对应的点到原点的距离,一般地,点![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() ,那么
,那么![]() 、
、![]() 之间的距离可表示为
之间的距离可表示为![]() .
.
(![]() )点
)点![]() 、
、![]() 、
、![]() 在数轴上分别表示有理数
在数轴上分别表示有理数![]() 、
、![]() 、
、![]() ,那么
,那么![]() 到
到![]() 的距离表示为______________________________(用含绝对值的式子表示).如果
的距离表示为______________________________(用含绝对值的式子表示).如果![]() ,那么
,那么![]() 为______________________________.
为______________________________.
(![]() )利用数轴探究:
)利用数轴探究:
①找出满足![]() 的
的![]() 的所有整数值是____________________;
的所有整数值是____________________;
②设![]() ,当
,当![]() 的值取在不小于
的值取在不小于![]() 且不大于
且不大于![]() 的范围时,
的范围时,![]() 的值是不变的,而且是
的值是不变的,而且是![]() 的最小值,这个最小值是____________________;
的最小值,这个最小值是____________________;
(![]() )求
)求![]() 的最小值为____________________,此时
的最小值为____________________,此时![]() 的值为____________________.
的值为____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“安全教育,警钟长鸣”,为此某校从14 000名学生中随机抽取了200名学生就安全知识的了解情况进行问卷调查,然后按“很好”、“较好”、“一般”、“较差”四类汇总分析,并绘制了扇形统计图(如图甲).
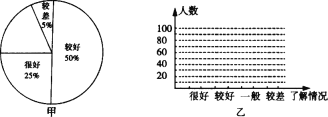
(1)补全扇形统计图,并计算这200名学生中对安全知识了解“较好”、“很好”的总人数;
(2)在图乙中,绘制样本频数的条形统计图;
(3)根据以上信息,请提出一条合理化建议.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一天,小明和小红玩纸片拼图游戏.发现利用图①中的三种材料各若干可以拼出一些图形来解释某些等式,比如图②可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图③可以解释为等式: .
(2)图④中阴影部分的面积为 .观察图④请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)如图⑤,小明利用7个长为b,宽为a的长方形拼成如图所示的大长方形;若AB=4,若长方形AGMB的面积与长方形EDHN的面积的差为S,试计算S的值(用含a,b的代数式表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(十九),用四个螺丝将四条不可弯曲的木条围成一个木框,不计螺丝大小,其中相邻两螺丝的距离依序为2、3、4、6,且相邻两木条的夹角均可调整。若调整木条的夹角时不破坏此木框,则任两螺丝的距离之最大值为何?

(A) 5 (B) 6 (C) 7 (D) 10
查看答案和解析>>
科目:初中数学 来源: 题型:
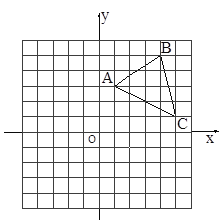
【题目】如图,在平面直角坐标系中,△ABC的三个顶点都在格点上,点A的坐标为(1,3),请解答下列问题:
(1)画出△ABC关于x轴对称的△A1B1C1,并写出点B1的坐标;
(2)画出△ABC绕原点O逆时针旋转90°后得到的△A2B2C2,并写出点C2的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com