
分析 (1)设大货车用x辆,小货车用y辆,根据大、小两种货车共18辆,运输192吨物资,列方程组求解;
(2)设前往甲地的大货车为x辆,则前往乙地的大货车为(10-x)辆,前往甲地的小货车为(10-x)辆,前往乙地的小货车为[10-(10-x)]辆,根据题意即可求出w与a的函数关系式;
(3)结合已知条件,求x的取值范围,由(2)的函数关系式求使总运费最少的货车调配方案.
解答 解:(1)设大车为x辆,小车为y辆,根据题意可得:
$\left\{\begin{array}{l}{x+y=18}\\{14x+8y=192}\end{array}\right.$,
解得:$\left\{\begin{array}{l}{x=8}\\{y=10}\end{array}\right.$,
答:这两种货车各8辆、10辆.
(2)设去甲地大货车x辆,根据题意可得:
y=720x+80(8-x)+500(10-x)+650[10-(10-x)]
=790x+5640(0≤x≤8且x为整数);
(3)14x+8(10-x)≥96,
解得x≥$\frac{8}{3}$,
又∵0≤x≤8,
∴3≤x≤8且为整数,
∵y=790x+5640,
k=790>0,y随x的增大而增大,
∴当x=3时,y最小,
y最小值为=790×3+5640=8010(元)
答:使总运费最少的调配方案是:3辆大货车、7辆小货车前往甲地;5辆大货车、3辆小货车前往乙地.最少运费为8010元.
点评 本题考查了一次函数的应用,二元一次方程组的应用.关键是根据题意,得出安排各地的大、小货车数与前往甲地的大货车数a的关系.


科目:初中数学 来源: 题型:解答题
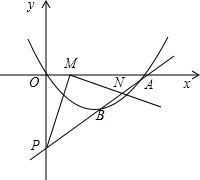 如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.
如图,抛物线y=ax2+bx+c过原点,且与直线y=mx+n交于A(8,0)、B(4,-3)两点,直线AB与y轴相交于点P,点M为线段OA上一动点,∠PMN为直角,边MN与AP相交于点N,设OM=t.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
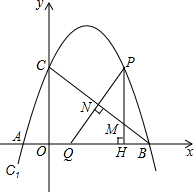 如图,抛物线C1:y=ax2+bx+3与x轴交于A、B(4,0)两点,与y轴交于点C,且AB=BC.
如图,抛物线C1:y=ax2+bx+3与x轴交于A、B(4,0)两点,与y轴交于点C,且AB=BC.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | a>$\frac{3}{2}$ | B. | a<-1 | C. | -1<x<$\frac{3}{2}$ | D. | 1<a<$\frac{3}{2}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
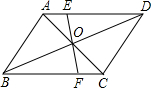 如图,在?ABCD中,EF过对角线交点O,交AD于E,交BC于F,若AB=4,BC=5,OE=1.5,那么,四边形EFCD的周长为( )
如图,在?ABCD中,EF过对角线交点O,交AD于E,交BC于F,若AB=4,BC=5,OE=1.5,那么,四边形EFCD的周长为( )| A. | 16 | B. | 14 | C. | 12 | D. | 10 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com