
【题目】如图,已知反比例函数y=![]() (k≠0)的图象与一次函数y=k'x+b(k'≠0)的图象相交于A和B两点。
(k≠0)的图象与一次函数y=k'x+b(k'≠0)的图象相交于A和B两点。
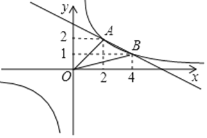
(1)求反比例函数和一次函数的表达式;
(2)观察两函数在同一坐标系中的图象,直接写出关于x的不等式![]() <k'x+b的解集;
<k'x+b的解集;
(3)求△AOB的面积.(其中O为坐标原点)
【答案】(1)反比例函数表达式为y=![]() ;一次函数表达式为y=
;一次函数表达式为y=![]() ;(2)x<0或2<x<4;(3)3
;(2)x<0或2<x<4;(3)3
【解析】
(1)运用待定系数法,根据A和B两点坐标即可得到反比例函数和一次函数的表达式;
(2)由函数图象的上下位置关系可得,不等式![]() <k′x+b的解集为x<0或2<x<4;
<k′x+b的解集为x<0或2<x<4;
(3)先求得直线AB与x轴的交点坐标,即可得到△AOB的面积.
(1)把A(2,2)代入反比例函数y=![]() (k≠0),可得,
(k≠0),可得,
k=2×2=4,
∴反比例函数的表达式为y=![]() ;
;
把A(2,2),B(4,1)代入一次函数y=k′x+b(k′≠0),可得
![]() ,
,
解得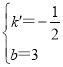 ,
,
∴一次函数的表达式为y=-![]() x+3;
x+3;
(2)由图可得,不等式![]() <k′x+b的解集为x<0或2<x<4.
<k′x+b的解集为x<0或2<x<4.
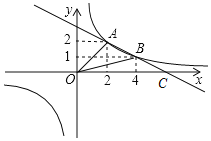
(3)在y=-![]() x+3中,令y=0,则0=-
x+3中,令y=0,则0=-![]() x+3,
x+3,
解得x=6,
∴C(6,0),
∴S△AOB=S△AOC-S△BOC
=![]() ×6×2-
×6×2-![]() ×6×1
×6×1
=6-3
=3.


科目:初中数学 来源: 题型:
【题目】已知:如图1,在△ABC中,点D在AB上,连接CD. DE平分∠BDC交BC于点E,且DE∥AC, 若F为AC的中点,连接DF.
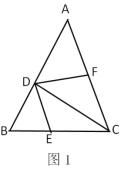
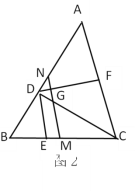
(1)求证:DF⊥DE.
(2)若BE:CE=2:3,S△CDE=9,求△ABC的面积.
(3)如图2,M为BC的中点,过M作MN∥DE交AB于点N,交CD于点G,若BD=a,DG=b.试求CD的长(用a、b的代数式表示).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,D是边AB上一点,且∠A=2∠DCB.E是BC边上的一点,以EC为直径的⊙O经过点D.
(1)求证:AB是⊙O的切线;
(2)若CD的弦心距为1,BE=EO,求BD的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,⊙O为△ABC的内切圆,切点分别为D、E、F,若AD=10,BC=5,则OB的长为( )
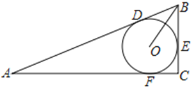
A.4B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点O是等边△ABC内的任一点,连接OA,OB,OC.
(1)如图1,已知∠AOB=150°,∠BOC=120°,将△BOC绕点C按顺时针方向旋转60°得△ADC.
①∠DAO的度数是 ;
②用等式表示线段OA,OB,OC之间的数量关系,并证明;
(2)设∠AOB=α,∠BOC=β.
①当α,β满足什么关系时,OA+OB+OC有最小值?请在图2中画出符合条件的图形,并说明理由;
②若等边△ABC的边长为1,直接写出OA+OB+OC的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关于x的方程ax2+(a+2)x+9a=0有两个不等的实数根x1,x2,且x1<1<x2,那么a的取值范围是( )
A.﹣![]() <a<
<a<![]() B.a>
B.a>![]() C.a<﹣
C.a<﹣![]() D.﹣
D.﹣![]() <a<0
<a<0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,四边形ABCD是菱形,点E在边CD上,点F在BC的延长线上,CF=DE,AE的延长线与DF相交于点G.
(1)求证:∠CDF=∠DAE;
(2)如果DE=CE,求证:AE=3EG.
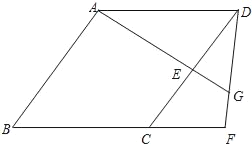
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个批发商销售成本为20元/千克的某产品,根据物价部门规定:该产品每千克售价不得超过90元,在销售过程中发现的售量y(千克)与售价x(元/千克)满足一次函数关系,对应关系如下表:
售价x(元/千克) | … | 50 | 60 | 70 | 80 | … |
销售量y(千克) | … | 100 | 90 | 80 | 70 | … |
(1)求y与x的函数关系式;
(2)该批发商若想获得4000元的利润,应将售价定为多少元?
(3)该产品每千克售价为多少元时,批发商获得的利润w(元)最大?此时的最大利润为多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】南沙群岛是我国固有领土,现在我南海渔民要在南沙某海岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向![]() 海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.
海里的C处,为了防止某国还巡警干扰,就请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向上,A位于B的北偏西30°的方向上,求A、C之间的距离.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com