
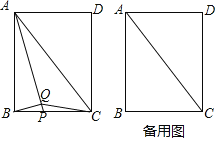
【题目】如图,在矩形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 为
为![]() 边上一动点,连结
边上一动点,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
(1)证明:![]() ;
;
(2)当点![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求
,求![]() 的度数;
的度数;
(3)当点![]() 运动到与点
运动到与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
【答案】(1)见解析;(2)53°;(3) ![]()
【解析】
(1)根据两角对应相等的两个三角形相似即可判断.
(2)只要证明△CPQ∽△APC,可得∠PQC=∠ACP即可解决问题.
(3)连接AF.与Rt△ADF≌Rt△AQF(HL),推出DF=QF,设AD=AQ=BC=m,DF=FQ=x,FC=y,CQ=a,证明△BCQ∽△CFQ,可得![]() ,推出
,推出![]() ,即
,即![]() ,由CF∥AB,可得
,由CF∥AB,可得![]() ,推出
,推出![]() ,可得
,可得![]() ,推出x2+xy-y2=0,解得x=
,推出x2+xy-y2=0,解得x=![]() y或
y或![]() (舍弃),由此即可解决问题.
(舍弃),由此即可解决问题.
(1)证明:∵四边形ABCD是矩形,
∴∠ABP=90°,
∵BQ⊥AP,
∴∠BQP=∠ABP=90°,
∵∠BPQ=∠APB,
∴△ABP∽△BQP.
(2)解:∵△ABP∽△BQP,
∴![]()
∴PB2=PQPA,
∵PB=PC,
∴PC2=PQPA,
∴![]()
∵∠CPQ=∠APC,
∴△CPQ∽△APC,
∴∠PQC=∠ACP,
∵∠BAC=37°,
∴∠ACB=90°-37°=53°,
∴∠CQP=53°.
(3)解:连接AF.
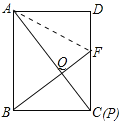
∵∠D=∠AQF=90°,AF=AF,AD=AQ,
∴Rt△ADF≌Rt△AQF(HL),
∴DF=QF,设AD=AQ=BC=m,DF=FQ=x,FC=y,CQ=a,
∵∠BCF=∠CQB=∠CQF=90°,
∴∠BCQ+∠FCQ=90°,∠CBQ=90°,
∴∠FCQ=∠CBQ,
∴△BCQ∽△CFQ,
∴![]() ,
,
∴![]()
∴![]() ,
,
∵CF∥AB,
∴![]() ,
,
∴![]()
∴![]()
∴x2+xy-y2=0,
∴ x=![]() y或
y或![]() (舍弃),
(舍弃),
∴![]()
∴![]() .
.
故答案为:![]() .
.


 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案科目:初中数学 来源: 题型:
【题目】某校八年级全体同学参加了某项捐款活动,随机抽查了部分同学捐款的情况统计如图所示.

(1)本次共抽查学生 人,并将条形图补充完整;
(2)捐款金额的众数是 平均数是 中位数为
(3)在八年级600名学生中,捐款20元及以上(含20元)的学生估计有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
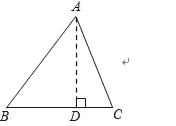
【题目】在△ABC中,AB=30,BC=28,AC=26.求△ABC的面积.
某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在△ABC中,∠A=30°,点P从点A出发以2cm/s的速度沿折线A﹣C﹣B运动,点Q从点A出发以a(cm/s)的速度沿AB运动,P,Q两点同时出发,当某一点运动到点B时,两点同时停止运动.设运动时间为x(s),△APQ的面积为y(cm2),y关于x的函数图象由C1,C2两段组成,如图2所示.
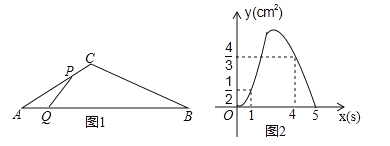
(1)求a的值;
(2)求图2中图象C2段的函数表达式;
(3)当点P运动到线段BC上某一段时△APQ的面积,大于当点P在线段AC上任意一点时△APQ的面积,求x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知AB=AD,那么添加下列一个条件后,仍无法判定△ABC≌△ADC的是( )

A. CB=CD B. ∠BAC=∠DAC C. ∠BCA=∠DCA D. ∠B=∠D=90°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整顿药品市场、降低药品价格是国家的惠民政策之一.根据国家《药品政府定价办法》,某省有关部门规定:市场流通药品的零售价格不得超过进价的15%.根据相关信息解决下列问题:
(1)降价前,甲乙两种药品每盒的出厂价格之和为6.6元.经过若干中间环节,甲种药品每盒的零售价格比出厂价格的5倍少2.2元,乙种药品每盒的零售价格是出厂价格的6倍,两种药品每盒的零售价格之和为33.8元.那么降价前甲、乙两种药品每盒的零售价格分别是多少元?
(2)降价后,某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院,医院根据实际情况决定:对甲种药品每盒加价15%、对乙种药品每盒加价10%后零售给患者.实际进药时,这两种药品均以每10盒为1箱进行包装.近期该医院准备从经销商处购进甲乙两种药品共100箱,其中乙种药品不少于40箱,销售这批药品的总利润不低于900元.请问购进时有哪几种搭配方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1)4![]() -[6
-[6![]() -2(4
-2(4![]() -2)-
-2)-![]() ]+1,其中
]+1,其中![]() =-
=-![]() y =1.
y =1.
(2)已知(a+2)2+|b-3|=0,求![]() (9ab2-3)+(7a2b-2)+2(ab2+1)-2a2b的值.
(9ab2-3)+(7a2b-2)+2(ab2+1)-2a2b的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com