
【题目】如图,![]() 是边长为2的等边三角形,
是边长为2的等边三角形,![]() 是
是![]() 延长线上一点,以
延长线上一点,以![]() 为边作等边三角形
为边作等边三角形![]() ,连接
,连接![]() .
.
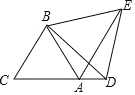
(1)求![]() 的度数.
的度数.
(2)求![]() 的值.
的值.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
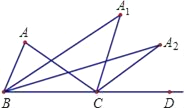
【题目】如图,在△ABC中,∠A=α,∠ABC的平分线与∠ACD的平分线交于点A1,得∠A1,则∠A1=_____.∠A1BC的平分线与∠A1CD的平分线交于点A2,得∠A2,…,∠A2009BC的平分线与∠A2009CD的平分线交于点A2010,得∠A2010,则∠A2010=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有20筐白菜,以每筐30千克为标准,超过千克数记作正数,不足的千克数记作负数,称后的记录如下表:
与标准质量的差值(单位:千克) |
|
|
| 0 | 1 | 2.5 |
筐数 | 1 | 4 | 4 | 2 | 3 | 6 |
(1)20筐白菜中,最重的一筐比最轻的一筐重 千克;
(2)与标准重量比较,20筐白菜总计超过或不足多少千克?
(3)若白菜每千克售价3.5元,则出售这20筐白菜可卖多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
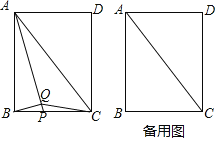
【题目】如图,在矩形![]() 中,
中,![]() 为对角线,点
为对角线,点![]() 为
为![]() 边上一动点,连结
边上一动点,连结![]() ,过点
,过点![]() 作
作![]() ,垂足为
,垂足为![]() ,连结
,连结![]() .
.
(1)证明:![]() ;
;
(2)当点![]() 为
为![]() 的中点时,若
的中点时,若![]() ,求
,求![]() 的度数;
的度数;
(3)当点![]() 运动到与点
运动到与点![]() 重合时,延长
重合时,延长![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,则
,则![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
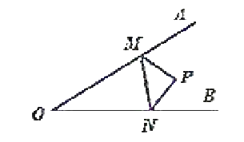
【题目】如图,![]() ,点
,点![]() 为
为![]() 内一点,
内一点,![]() ,点
,点![]() 分别在射线
分别在射线![]() 上,当
上,当![]() 的周长最小时,下列结论:①
的周长最小时,下列结论:①![]() ;②
;②![]() ;③
;③![]() 的周长最小值为24;④
的周长最小值为24;④![]() 的周长最小值为8;其中正确的序号为__________.
的周长最小值为8;其中正确的序号为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法错误的有( )个
①互为相反数的数的立方根也互为相反数;
②![]() 不是整式;
不是整式;
③算术平方根等于它本身的数只有零;
④实数和数轴上的点一一对应;
⑤任何两数相加,和不小于任何一个加数.
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图 ,已知△ ABC 中,点 D 、E 是 BC 边上两点,且 ADAE ,BAECAD 90 ,
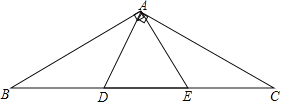
(1)试说明△ABE 与△ACD 全等的理由;
(2)如果 ADBD ,试判断△ADE 的形状,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一次数学活动中,小辉将一块矩形纸片![]() 对折,使
对折,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开,再一次折叠纸片,使点
,把纸片展开,再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() .同时,得到了线段
.同时,得到了线段![]() .
.
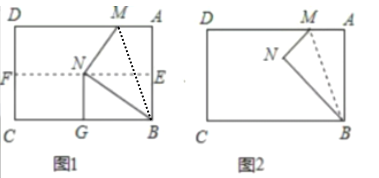
(1)如图![]() ,若点
,若点![]() 刚好落在折痕
刚好落在折痕![]() 上时,
上时,
①过![]() 作
作![]() ,求证:
,求证:![]() ;
;
②求![]() 的度数;
的度数;
(2)如图![]() ,当
,当![]() 为射线
为射线![]() 上的一个动点时,已知
上的一个动点时,已知![]() ,
,![]() ,若
,若![]() 的直角三角形时,请直接写出
的直角三角形时,请直接写出![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
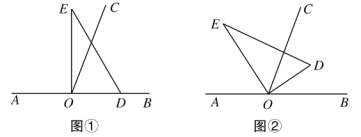
【题目】如图,以直线AB上一点O为端点作射线OC,使∠BOC=70°,将一个直角三角板的直角顶点放在点O处(∠DOE=90°).
(1)如图①,若直角三角板DOE的一边OD放在射线OB上,则∠COE= °;
(2)如图②,将直角三角板DOE绕点O转动,若OD恰好平分∠BOC,求∠AOE的度数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com