
【题目】在一次数学活动中,小辉将一块矩形纸片![]() 对折,使
对折,使![]() 与
与![]() 重合,得到折痕
重合,得到折痕![]() ,把纸片展开,再一次折叠纸片,使点
,把纸片展开,再一次折叠纸片,使点![]() 落在
落在![]() 上,并使折痕经过点
上,并使折痕经过点![]() ,得到折痕
,得到折痕![]() .同时,得到了线段
.同时,得到了线段![]() .
.
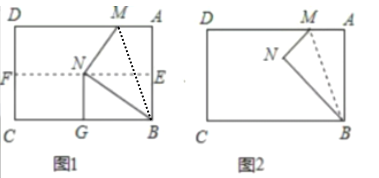
(1)如图![]() ,若点
,若点![]() 刚好落在折痕
刚好落在折痕![]() 上时,
上时,
①过![]() 作
作![]() ,求证:
,求证:![]() ;
;
②求![]() 的度数;
的度数;
(2)如图![]() ,当
,当![]() 为射线
为射线![]() 上的一个动点时,已知
上的一个动点时,已知![]() ,
,![]() ,若
,若![]() 的直角三角形时,请直接写出
的直角三角形时,请直接写出![]() 的长.
的长.
【答案】(1)①见解析;②![]() ;(2)
;(2)![]() 或
或![]() .
.
【解析】
(1)①连接AN,首先由折叠易知△ABM≌△NBM,且EF⊥AB,E为AB中点,从而证得△BAN为等边三角形,利用等边三角形的性质得到∠NBG=30°即可;;
②由①可得∠NBM=30°,从而求得∠BMN=60°,即可求得∠AMN的值;
(2)根据四边形ABCD为矩形得到∠A=∠MNB=90°,然后分当∠NBC=90°、当∠BNC=90° N在矩形ABCD内部、当∠BNC=90° N在矩形ABCD外部时三种情况利用勾股定理求得结论即可.
①证明:连接AN,
∵由折叠易知△ABM≌△NBM,且EF⊥AB,E为AB中点,
∴AB=BN,NA=BN,
∴△BAN为等边三角形,
∴∠ABN=60°,
∵∠ABC=90°,
∴∠NBG=30°;
∵![]() ∠NGB=90°,
∠NGB=90°,
∴![]()
②由①得:△BAN为等边三角形,
∴∠ABN=60°,
由折叠得,∠NBM=∠ABM=30°,∠MNB=∠BAM=90°,
∴∠BMN=∠BMA=60°.
∴![]() =120°
=120°
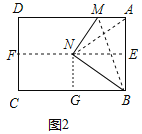
(2)∵四边形ABCD为矩形,
∴∠A=∠MNB=90°,
①当∠NBC=90°,∠NCB=90°都不符合题意,舍去,
②当∠BNC=90°,N在矩形ABCD内部,
∵∠BNC=∠MNB=90°,
∴M、N、C三点共线,
∵AB=BN=3,BC=5,∠BNC=90°
∴NC=4
设AM=MN=x
∵MD=5-x,MC=4+x,
∴在Rt△MDC中,CD2+MD2=MC2,
32+(5-x)2=(4+x)2,
解得x=1;
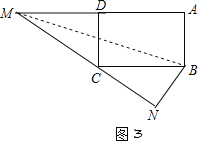
③当∠BNC=90° N在矩形ABCD外部时,
∵∠BNC=∠MNB=90°,
∴M、C、N三点共线,
∵AB=BN=3,BC=5,∠BNC=90°,
∴NC=4,
设AM=MN=y,
∵MD=y-5,MC=y-4,
∴在Rt△MDC中 ,CD2+MD2=MC2
32+(y-5)2=(y-4)2,
解得y=9,
综上所述:当AM=1或9时△NBC是直角三角形.


科目:初中数学 来源: 题型:
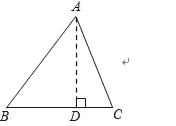
【题目】在△ABC中,AB=30,BC=28,AC=26.求△ABC的面积.
某学习小组经过合作交流给出了下面的解题思路,请你按照他们的解题思路完成解答过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】整顿药品市场、降低药品价格是国家的惠民政策之一.根据国家《药品政府定价办法》,某省有关部门规定:市场流通药品的零售价格不得超过进价的15%.根据相关信息解决下列问题:
(1)降价前,甲乙两种药品每盒的出厂价格之和为6.6元.经过若干中间环节,甲种药品每盒的零售价格比出厂价格的5倍少2.2元,乙种药品每盒的零售价格是出厂价格的6倍,两种药品每盒的零售价格之和为33.8元.那么降价前甲、乙两种药品每盒的零售价格分别是多少元?
(2)降价后,某药品经销商将上述的甲、乙两种药品分别以每盒8元和5元的价格销售给医院,医院根据实际情况决定:对甲种药品每盒加价15%、对乙种药品每盒加价10%后零售给患者.实际进药时,这两种药品均以每10盒为1箱进行包装.近期该医院准备从经销商处购进甲乙两种药品共100箱,其中乙种药品不少于40箱,销售这批药品的总利润不低于900元.请问购进时有哪几种搭配方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)你认为图②中的阴影部分的正方形的边长等于_________________;
(2)请用两种不同的方法列代数式表示图②中阴影部分的面积.
方法① __________________.方法② _____________________;
(3)观察图②,你能写出(m+n)2,(m-n)2,mn这三个代数式之间的等量关系吗?
答:________________________ .
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=4,则求(a-b)2的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为举办校园文化艺术节,甲、乙两班准备给合唱同学购买演出服装(一人一套),两班共92人(其中甲班比乙班人多,且甲班不到90人),下面是供货商给出的演出服装的价格表:
购买服装的套数 | 1套至45套 | 46套至90套 | 91套以上 |
每套服装的价格 | 60元 | 50元 | 40元 |
如果两班单独给每位同学购买一套服装,那么一共应付5020元.
(1)甲、乙两班联合起来给每位同学购买一套服装,比单独购买可以节省多少钱?
(2)甲、乙两班各有多少名同学?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】化简求值:
(1)4![]() -[6
-[6![]() -2(4
-2(4![]() -2)-
-2)-![]() ]+1,其中
]+1,其中![]() =-
=-![]() y =1.
y =1.
(2)已知(a+2)2+|b-3|=0,求![]() (9ab2-3)+(7a2b-2)+2(ab2+1)-2a2b的值.
(9ab2-3)+(7a2b-2)+2(ab2+1)-2a2b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
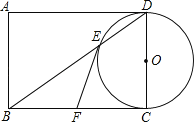
【题目】如图,以矩形ABCD的边CD为直径作⊙O,交矩形的对角线BD于点E,点F是BC的中点,连接EF.
(1)试判断EF与⊙O的位置关系,并说明理由.
(2)若DC=2,EF=![]() ,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
,点P是⊙O上不与E、C重合的任意一点,则∠EPC的度数为 (直接写出答案)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com