
【题目】阅读理解:
我们已经学习的直角三角形知识包括:勾股定理,30°、45°特殊角的直角三角形的边之间的关系等,在解决初中数学问题上起到重要作用,锐角三角函数是另一个研究直角三角形中边角间关系的知识,通过锐角三角函数也可以帮助解决数学问题.
阅读下列材料,完成习题:
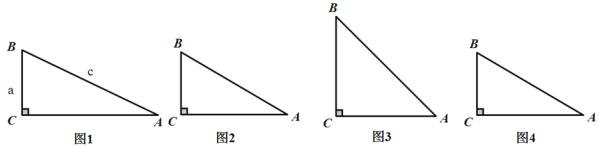
如图1,在Rt△ABC中,∠C=90°,我们把锐角A的对边与斜边的比叫做∠A的正弦(sine),记作sinA,即sinA=![]()
例如:a=3,c=7,则sinA=![]()
问题:在Rt△ABC中,∠C=90°
(1)如图2,BC=5,AB=8,求sinA的值.
(2)如图3,当∠A=45°时,求sinB的值.
(3)AC=2![]() ,sinB=
,sinB=![]() ,求BC的长度.
,求BC的长度.
科目:初中数学 来源: 题型:
【题目】为配合我市创建省级文明城市,某校对八年级各班文明行为劝导志愿者人数进行了统计,各班统计人数有6名、5名、4名、3名、2名、1名共计六种情况,并制作如下两幅不完整的统计图. 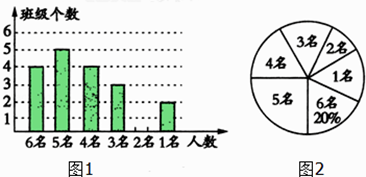
(1)求该年级平均每班有多少文明行为劝导志愿者?并将条形图补充完整;
(2)该校决定本周开展主题实践活动,从八年级只有2名文明行为劝导志愿者的班级中任选两名,请用列表或画树状图的方法,求出所选文明行为劝导志愿者有两名来自同一班级的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C、G是⊙O上两点,且AC=CG,过点C的直线CD⊥BG于点D,交BA的延长线于点E,连接BC,交OD于点F. 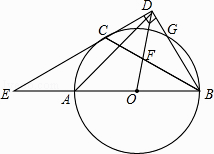
(1)求证:CD是⊙O的切线.
(2)若 ![]() ,求∠E的度数.
,求∠E的度数.
(3)连接AD,在(2)的条件下,若CD= ![]() ,求AD的长.
,求AD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
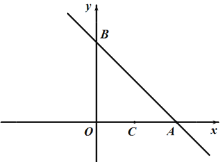
【题目】如图,直线y=-x+4分别与x轴、y轴交于A、B两点.
(1)求A、B两点的坐标;
(2)已知点C坐标为(2,0),设点C关于直线AB的对称点为D,请直接写出点D的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点的门票零售价为80元/张,“五一”黄金周期间,甲乙两家旅行社推出优惠活动,甲旅行社一律九折优惠;乙旅行社对10人以内(含10人)不优惠,超过10人超出部分八折优惠,某班部分同学去该景点旅游.设参加旅游人数为x人,购买门票需要y元.
(1)分别直接写出两家旅行社y与x的函数关系式,并写出对应自变量x的取值范围;
(2)请根据该班旅游人数设计最省钱的购票方案.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c(a≠0)的图象经过点(1,2)且与x轴交点的横坐标分别为x1 , x2 , 其中﹣1<x1<0,1<x2<2,下列结论:4a+2b+c<0,2a+b<0,b2+8a>4ac,a<﹣1,其中结论正确的有( ) 
A.1个
B.2个
C.3个
D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
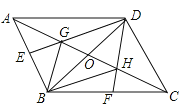
【题目】如图,已知G、H是△ABC的边AC的三等分点,GE∥BH,交AB于点E,HF∥BG交BC于点F,延长EG、FH交于点D,连接AD、DC,设AC和BD交于点O,求证:四边形ABCD是平行四边形.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com