Question

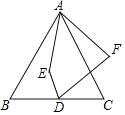
【题目】如图，等边△ABC中，AB=10，D为BC的中点，E为△ABC内一动点，DE=3，连接AE，将线段AE绕点A逆时针旋转60°得AF，连接DF，求线段DF的最小值.

Answer 1

【答案】5-3

【解析】

以ED为边作等边△DEG，连接AD，EF，AG，由等边三角形的性质和勾股定理可求AD=5，由等边三角形的性质可证△AEG≌△FED，可得DF=AG，根据三角形的三边关系，可得当点A，点G，点D三点共线时，AG值最小，即DF值最小，则可求线段DF的最小值．

如图，以ED为边作等边△DEG，连接AD，EF，AG，

∵△ABC是等边三角形，点D是BC中点，

∴BD=CD=5，AD⊥BC

∴AD==5，

∵将线段AE绕点A逆时针旋转60°得AF，

∴AE=AF，∠EAF=60°，

∴△AEF是等边三角形，

∴AE=EF，∠AEF=60°，

∵△DEG是等边三角形

∴DE=EG=3，∠GED=60°=∠AEF

∴∠AEG=∠FED，且AE=EF，EG=DE，

∴△AEG≌△FED（SAS）

∴DF=AG，

∵在△ADG中，AG≥AD-DG

∴当点A，点G，点D三点共线时，AG值最小，即DF值最小，

∴DF最小值=AD-DG=5-3