
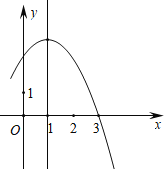
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(3,0),且对称轴为直线x=1.下列说法,其中正确的是( )
①abc<0
②b2﹣4ac>0;
③a﹣b+c<0;
④b﹣c>2a
A.①②B.①③④C.②④D.①②④
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】某厂大门是抛物线形水泥建筑,大门地面路宽为6![]() ,顶部距离地面的高度为4
,顶部距离地面的高度为4![]() ,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4
,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4![]() ,要想通过此门,则设备及车辆总高度应小于______.
,要想通过此门,则设备及车辆总高度应小于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们规定:如果一个三角形有一边上的中线等于这条边的一半,那么称这个三角形为“智慧三角形”.
理解:
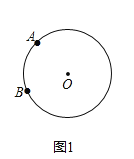
(1)如图1,已知A、B是⊙O上两点,请在圆上找出满足条件的点C,使△ABC为“智慧三角形”(画出点C的位置,保留作图痕迹);
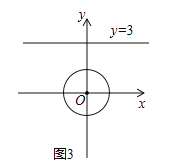
(2)如图3,在平面直角坐标系xOy中,⊙O的半径为1,点Q是直线y=3上的一点,若在⊙O上存在一点P,使得△OPQ为“智慧三角形”,当其面积取得最小值时,直接写出此时PQ的长和点Q的坐标
查看答案和解析>>
科目:初中数学 来源: 题型:
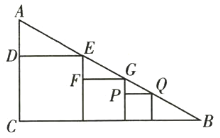
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 内有三个正方形,且这三个正方形都有一边在
内有三个正方形,且这三个正方形都有一边在![]() 上,都有一个顶点在
上,都有一个顶点在![]() 上,点
上,点![]() 在
在![]() 上,第一个正方形边
上,第一个正方形边![]() 长
长![]() ,第二个正方形边
,第二个正方形边![]() 长
长![]() ,那么第三个正方形的边
,那么第三个正方形的边![]() 长为______.
长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
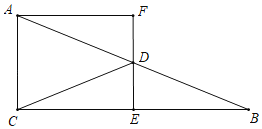
【题目】Rt△ABC中,∠ACB=90°,点D是AB中点,连CD,过点D作DE⊥BC于E,过A作AF⊥ED的延长线于F.
(1)若∠B=25°,求∠ADC的度数;
(2)求证:DF=DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
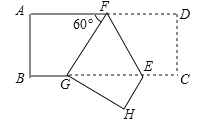
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a,b,c为常数,且a≠0)中的x与y的部分对应值如下表:

下列结论:(1)ac<0;(2)当x>1时,y的值随x值的增大而减小.(3)3是方程ax2+(b![]() )x+c=0的一个根;(4)当
)x+c=0的一个根;(4)当![]() <x<3时,ax2+(b
<x<3时,ax2+(b![]() )x+c>0.其中正确的个数为( )
)x+c>0.其中正确的个数为( )
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
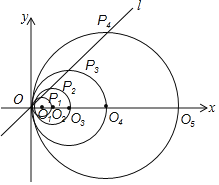
【题目】如图,在平面直角坐标系中,直线l的函数表达式为y=x,点O1的坐标为(1,0),以O1为圆心,O1O为半径画圆,交直线l于点P1,交x轴正半轴于点O2,以O2为圆心,O2O为半径画圆,交直线l于点P2,交x轴正半轴于点O3,以O3为圆心,O3O为半径画圆,交直线l于点P3,交x轴正半轴于点O4;…按此做法进行下去,其中![]() 的长为_____.
的长为_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com