
【题目】在正方形ABCD中,P是BC上一点,且BP=3PC,Q是CD的中点.
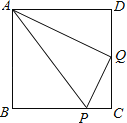
(1)求证:△ADQ∽△QCP;
(2)若PQ=3,求AP的长.
【答案】(1)见解析;(2)3![]()
【解析】
(1)在所要求证的两个三角形中,已知的等量条件为:∠D=∠C=90°,若证明两三角形相似,可证两个三角形的对应直角边成比例;
(2)证明AQ=2PQ,AQ⊥PQ即可解决问题.
(1)证明:∵四边形ABCD是正方形,
∴AD=CD,∠C=∠D=90°;
又∵Q是CD中点,
∴CQ=DQ=![]() AD;
AD;
∵BP=3PC,
∴CP=![]() AD,
AD,
∴![]() =
=![]() =
=![]() ,
,
又∵∠C=∠D=90°,
∴△ADQ∽△QCP;
(2)由(1)知,△ADQ∽△QCP,![]() =
=![]() =
=![]() ,
,
∴AQ=2PQ,
∵PQ=3,
∴AQ=6,
∵△ADQ∽△QCP,
∴∠AQD=∠QPC,∠DAQ=∠PQC,
∴∠PQC+∠DQA=DAQ+AQD=90°,
∴AQ⊥QP,
∴∠AQP=90°,
∴PA=![]() =3
=3![]() .
.



 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:
【题目】矩形ABCD与CEFG,如图放置,点B,C,E共线,点C,D,G共线,连接AF,取AF的中点H,连接GH.若BC=EF=2,CD=CE=1,则GH=( )

A. 1 B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
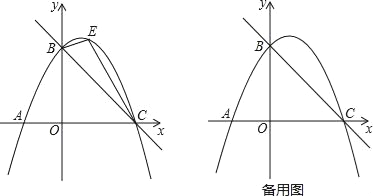
【题目】如图,直线y=﹣2x+3与x轴交于点C,与y轴交于点B,抛物线y=ax2+x+c经过B、C两点.
(1)求抛物线的解析式;
(2)如图,点E是直线BC上方抛物线上的一动点,当△BEC面积最大时,请求出点E的坐标和△BEC面积的最大值?
(3)在(2)的结论下,过点E作y轴的平行线交直线BC于点M,连接AM,点Q是抛物线对称轴上的动点,在抛物线上是否存在点P,使得以P、Q、A、M为顶点的四边形是平行四边形?如果存在,请直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=3x2+bx+c与直线y=﹣1只有一个公共点M,与平行于x轴的直线l交此抛物线A,B两点若AB=4,则点M到直线l的距离为( )
A.11B.12C.![]() D.13
D.13
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1,且m≠0.
(1)求抛物线的顶点坐标;
(2)试说明抛物线与直线有两个交点;
(3)已知点T(t,0),且-1≤t≤1,过点T作x轴的垂线,与抛物线交于点P,与直线交于点Q,当0<m≤3时,求线段PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
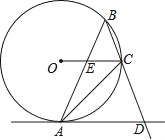
【题目】如图⊙O是△ABC的外接圆,∠ABC=45°,延长BC于D,连接AD,使得AD∥OC,AB交OC于E.
(1)求证:AD与⊙O相切;
(2)若AE=2![]() ,CE=2.求⊙O的半径和AB的长度.
,CE=2.求⊙O的半径和AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
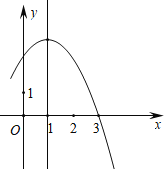
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(3,0),且对称轴为直线x=1.下列说法,其中正确的是( )
①abc<0
②b2﹣4ac>0;
③a﹣b+c<0;
④b﹣c>2a
A.①②B.①③④C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】花园小区有一朝向为正南方向的居民楼(如图),该居民楼的一楼是高4米的小区商场,商场以上是居民住房.在该楼的前面16米处要盖一栋高18米的办公楼.当冬季正午的阳光与水平线的夹角为![]() 时,问:
时,问:
(1)商场以上的居民住房采光是否有影响,为什么?
(2)若要使商场采光不受影响,两楼应相距多少 米?(结果保留一位小数)
(参考数据:![]() ,
,![]() ,
,![]() )
)

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com