
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 内有三个正方形,且这三个正方形都有一边在
内有三个正方形,且这三个正方形都有一边在![]() 上,都有一个顶点在
上,都有一个顶点在![]() 上,点
上,点![]() 在
在![]() 上,第一个正方形边
上,第一个正方形边![]() 长
长![]() ,第二个正方形边
,第二个正方形边![]() 长
长![]() ,那么第三个正方形的边
,那么第三个正方形的边![]() 长为______.
长为______.
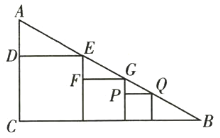
【答案】4cm
【解析】
根据正方形的性质可得:EM=DE=9cm,GN=GF=FM=6cm,PN=PQ,∠EFG=∠GPQ=90°,FG∥CB,PQ∥CB,设PN=PQ=x,从而求出EF=EM-FM=3cm,GP=GN-PN=(6-x)cm,FG∥PQ,利用相似三角形的判定可得:△EGF∽△GQP,根据相似三角形的性质列出比例式,即可求出x.
解:设这三个正方形落在BC上的其它点分别为M、N、H
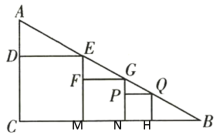
∴EM=DE=9cm,GN=GF=FM=6cm,PN=PQ,∠EFG=∠GPQ=90°,FG∥CB,PQ∥CB
设PN=PQ=x
∴EF=EM-FM=3cm,GP=GN-PN=(6-x)cm,FG∥PQ
∴∠EGF=∠GQP
∴△EGF∽△GQP
∴![]()
即:![]()
解得:x=4
即第三个正方形的边![]() 长为:4cm.
长为:4cm.
故答案为:4cm.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,二次函数![]() 的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.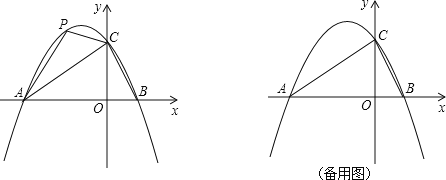
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果把函数y=x2(x≤2)的图象和函数y=![]() 的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
的图象组成一个图象,并称作图象E,那么直线y=3与图象E的交点有_____个;若直线y=m(m为常数)与图象E有三个不同的交点,则常数m的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=mx2+2mx+m-1和直线y=mx+m-1,且m≠0.
(1)求抛物线的顶点坐标;
(2)试说明抛物线与直线有两个交点;
(3)已知点T(t,0),且-1≤t≤1,过点T作x轴的垂线,与抛物线交于点P,与直线交于点Q,当0<m≤3时,求线段PQ长的最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(操作发现)如图(1),在△OAB和△OCD中,OA=OB,OC=OD,∠AOB=∠COD=45°,连接AC,BD交于点M.
①AC与BD之间的数量关系为 ;
②∠AMB的度数为 ;
(类比探究)如图(2),在△OAB和△OCD中,∠AOB=∠COD=90°,∠OAB=∠OCD=30°,连接AC,交BD的延长线于点M.请计算![]() 的值及∠AMB的度数;
的值及∠AMB的度数;
(实际应用)如图(3),是一个由两个都含有30°角的大小不同的直角三角板ABC、DCE组成的图形,其中∠ACB=∠DCE=90°,∠A=∠D=30°且D、E、B在同一直线上,CE=1,BC=![]() ,求点A、D之间的距离.
,求点A、D之间的距离.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)过点(3,0),且对称轴为直线x=1.下列说法,其中正确的是( )
①abc<0
②b2﹣4ac>0;
③a﹣b+c<0;
④b﹣c>2a
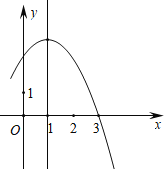
A.①②B.①③④C.②④D.①②④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于任意一个自然数N,将其各个数位上的数字相加得到一个数,我们把这一过程称为一次操作,把这个得到的数进行同样的操作,不断进行下去,最终会得到一个一位数K,我们把K称为N的“终极数”,并记f(N)=K.例如,456→4+5+6=15→1+5=6,∴f(456)=6.
(1)计算:f(2019)= .f(20192020)= .
(2)有一个三位自然数M=![]() ,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
查看答案和解析>>
科目:初中数学 来源: 题型:
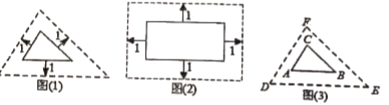
【题目】某校九年级数学兴趣小组在研究相似多边形问题时,他们提出了两个观点:
观点一:将外面大三角形按图1的方式向内缩小,得到新三角形,它们的对应边间距都为1,则新三角形与原三角形相似.
观点二:将邻边为6和10的矩形按图2的方式向外扩张,得到新的矩形,它们的对应边间距都为1,则新矩形与原矩形相似.
请回答下列问题:
(1)你认为上述两个观点是否正确,说明理由.
(2)如图3,若![]() 的周长和面积都是24,
的周长和面积都是24,![]() ,将
,将![]() 按图3的方式向外扩张,得到
按图3的方式向外扩张,得到![]() ,它们的对应边间距都为
,它们的对应边间距都为![]() ,
,![]() ,求
,求![]() 的周长和面积.
的周长和面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com