
【题目】在平面直角坐标系中,二次函数![]() 的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
的图象与x轴交于A(-3,0),B(1,0)两点,与y轴交于点C.
(1)求这个二次函数的关系解析式;
(2)点P是直线AC上方的抛物线上一动点,是否存在点P,使△ACP的面积最大?若存在,求出点P的坐标;若不存在,说明理由;
考生注意:下面的(3)、(4)、(5)题为三选一的选做题,即只能选做其中一个题目,多答时只按作答的首题评分,切记啊!
(3)在平面直角坐标系中,是否存在点Q,使△BCQ是以BC为腰的等腰直角三角形?若存在,直接写出点Q的坐标;若不存在,说明理由;
(4)点Q是直线AC上方的抛物线上一动点,过点Q作QE垂直于x轴,垂足为E.是否存在点Q,使以点B、Q、E为顶点的三角形与△AOC相似?若存在,直接写出点Q的坐标;若不存在,说明理由;
(5)点M为抛物线上一动点,在x轴上是否存在点Q,使以A、C、M、Q为顶点的四边形是平行四边形?若存在,直接写出点Q的坐标;若不存在,说明理由.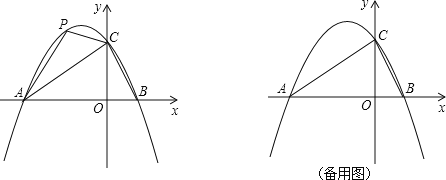
【答案】(1)![]() ;(2)存在,
;(2)存在,![]() ;(3)存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(1,1),Q4(2,1);(4)存在,Q点坐标为(2,2)或
;(3)存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(1,1),Q4(2,1);(4)存在,Q点坐标为(2,2)或![]() ;(5)存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.Q点坐标为:
;(5)存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.Q点坐标为:![]() .
.
【解析】
(1)将点A、B的坐标代入![]() 即可求得a、b,从而得到二次函数的关系解析式.
即可求得a、b,从而得到二次函数的关系解析式.
(2)设点P坐标为(m,n),则![]() .连接PO,作PM⊥x轴于M,PN⊥y轴于N,根据
.连接PO,作PM⊥x轴于M,PN⊥y轴于N,根据![]() 求出S关于m的二次函数,根据二次函数最值求法即可求解.
求出S关于m的二次函数,根据二次函数最值求法即可求解.
(3)如图(3)所示,以BC为边,在线段BC两侧分别作正方形,正方形的其他四个顶点均可以使得“△BCQ是以BC为腰的等腰直角三角形”,因此有四个点符合题意要求;
(4)如图(4)所示,若以点B、Q、E为顶点的三角形与△AOC相似,有两种情况,需要分类讨论,不要漏解;
(5)以A、C、M、Q为顶点的四边形是平行四边形,有四种情况,分别如图(5)a、图(5)b所示,注意不要漏解.
解:(1)由抛物线![]() 过A(-3,0),B(1,0),则
过A(-3,0),B(1,0),则
![]() ,解得
,解得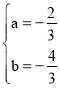 .
.
∴二次函数的关系解析式为![]() .
.
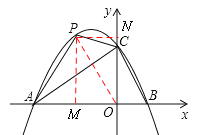
(2)设点P坐标为(m,n),则![]() .
.
连接PO,作PM⊥x轴于M,PN⊥y轴于N.
PM =![]() ,
,![]() ,AO=3.
,AO=3.
当![]() 时,
时,![]() ,所以OC=2.
,所以OC=2.
![]()
![]()
∵![]() <0,∴函数
<0,∴函数![]() 有最大值,当
有最大值,当![]() 时,
时,![]() 有最大值.
有最大值.
此时![]() .
.
∴存在点![]() ,使△ACP的面积最大.
,使△ACP的面积最大.
(3)如图(3)所示,以BC为边在两侧作正方形BCQ1Q2、正方形BCQ4Q3,则点Q1,Q2,Q3,Q4为符合题意要求的点.
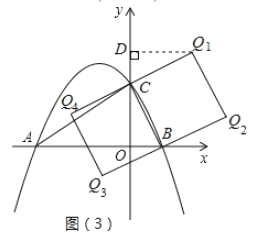
过Q1点作Q1D⊥y轴于点D,
∵∠BCQ1=90°,
∴∠Q1CD+∠OCB=90°,
又∵在直角△OBC中,∠OCB+∠CBO=90°,
∴∠Q1CD=∠OCB,
又∵Q1C=BC,∠Q1DC=∠BOC,
∴△Q1CD≌△CBO,
∴Q1D=OC=2,CD=OB=1,∴OD=OC+CD=3,∴Q1(2,3);
同理求得Q2(3,1),Q3(1,1),Q4(2,1).
∴存在点Q,使△BCQ是以BC为腰的等腰直角三角形.Q点坐标为:Q1(2,3),Q2(3,1),Q3(1,1),Q4(2,1).
(4)如图(4)所示,设E(n,0),则BE=1n, ![]() .
.

假设以点B.Q、E为顶点的三角形与△AOC相似,则有两种情况:
①若△AOC∽△BEQ,则有:![]() ,
,
即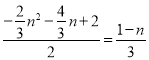 ,化简得:n2+n2=0,
,化简得:n2+n2=0,
解得n1=2,n2=1(与B重合,舍去),
∴n=2, ![]() .
.
∴Q(2,2);
②若△AOC∽△BQE,则有:![]() ,
,
即 ,化简得:4n2n3=0,
,化简得:4n2n3=0,
解得![]() (与B重合,舍去),
(与B重合,舍去),
![]()
∴![]() .
.
综上所述,存在点Q,使以点B.Q、E为顶点的三角形与△AOC相似.
Q点坐标为(2,2)或![]() .
.
(5)假设存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.
①若CM平行于x轴,如图(5)a所示,有符合要求的两个点Q1,Q2,此时Q1A=Q2A=CM.
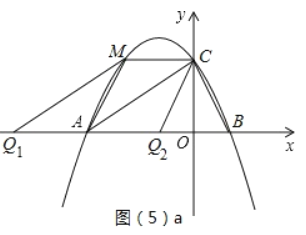
∵CM∥x轴,∴点M、点C(0,2)关于对称轴x=1对称,
∴M(2,2),
∴CM=2.
由Q1A=Q2A=CM=2,得到Q1(5,0),Q2(1,0);
②若CM不平行于x轴,如图(5)b所示.过点M作MG⊥x轴于G,
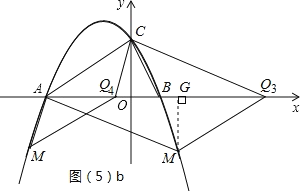
易证△MGQ≌△COA,得QG=OA=3,MG=OC=2,即yM=2.
设M(x,2),则有![]() ,
,
解得![]()
又QG=3,
∴![]() ,
,
![]()
综上所述,存在点Q,使以A. C.M、Q为顶点的四边形是平行四边形.Q点坐标为:![]() .
.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案科目:初中数学 来源: 题型:
【题目】某年级组织学生参加夏令营活动,本次夏令营分为甲、乙、丙三组进行活动.下面两幅统计图反映了学生报名参加夏令营的情况,请你根据图中的信息回答下列问题:
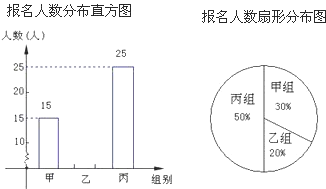
(1)该年级报名参加丙组的人数为 ;
(2)该年级报名参加本次活动的总人数 ,并补全频数分布直方图;
(3)根据实际情况,需从甲组抽调部分同学到丙组,使丙组人数是甲组人数的3倍,应从甲组抽调多少名学生到丙组?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系xOy中,有AB为斜边的等腰直角三角形ABC,其中点A(0,2),点C(﹣1,0),抛物线y=ax2+ax﹣2经过B点.
(1)求B点的坐标;
(2)求抛物线的解析式;
(3)在抛物线上是否存在点N(点B除外),使得△ACN仍然是以AC为直角边的等腰直角三角形?若存在,求点N的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2+(2k+1)x+k2=0①有两个不相等的实数根.
(1)求k的取值范围;
(2)设方程①的两个实数根分别为x1,x2,当k=1时,求x12+x22的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某厂大门是抛物线形水泥建筑,大门地面路宽为6![]() ,顶部距离地面的高度为4
,顶部距离地面的高度为4![]() ,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4
,现有一辆装载大型设备的车辆要进入厂区,已知设备总宽为2.4![]() ,要想通过此门,则设备及车辆总高度应小于______.
,要想通过此门,则设备及车辆总高度应小于______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.直角尺的直角顶点放在点P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).
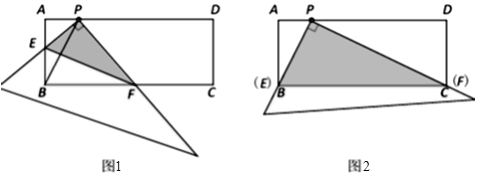
(1)当点E与点B重合时,点F恰好与点C重合(如图2).
①求证:△APB∽△DCP;
②求PC、BC的长.
(2)探究:将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中(图1是该过程的某个时刻),观察、猜想并解答:
① tan∠PEF的值是否发生变化?请说明理由.
② 设AE=x,当△PBF是等腰三角形时,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在同一平面内,将△ABC绕A点逆时针旋转到△ADE的位置.若AC⊥DE,∠ABD=62°,则∠ACB的度数为( )
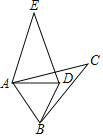
A.56°B.44°C.34°D.40°
查看答案和解析>>
科目:初中数学 来源: 题型:
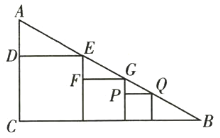
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 内有三个正方形,且这三个正方形都有一边在
内有三个正方形,且这三个正方形都有一边在![]() 上,都有一个顶点在
上,都有一个顶点在![]() 上,点
上,点![]() 在
在![]() 上,第一个正方形边
上,第一个正方形边![]() 长
长![]() ,第二个正方形边
,第二个正方形边![]() 长
长![]() ,那么第三个正方形的边
,那么第三个正方形的边![]() 长为______.
长为______.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com