
【题目】对于任意一个自然数N,将其各个数位上的数字相加得到一个数,我们把这一过程称为一次操作,把这个得到的数进行同样的操作,不断进行下去,最终会得到一个一位数K,我们把K称为N的“终极数”,并记f(N)=K.例如,456→4+5+6=15→1+5=6,∴f(456)=6.
(1)计算:f(2019)= .f(20192020)= .
(2)有一个三位自然数M=![]() ,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
,已知f(M)=4,且x<y<z,请求出所有满足条件的自然数M.
【答案】(1)3,7;(2)有满足条件的M为139,148,157,238,247,256,346,589,678.
【解析】
(1)由题意直接可求;
(2)由已知条件得到4=0+4=1+3=2+2,即z+y+z的值为4或13或22,再结合x<y<z,即可求解.
解:(1)由题意可知,2019→2+0+1+9=12→1+2=3,
∴f(2019)=3;
20192020→2+0+1+9+2+0+2+0=16→1+6=7,
∴f(20192020)=7;
故答案为3,7;
(2)∵三位自然数M=![]() ,f(M)=4,
,f(M)=4,
∵4=0+4=1+3=2+2,
当4=0+4时,x+y+z=4,或x+y+z=40(舍),
∵x<y<z,
∴x=0,y=1,z=3,此时不符题意;
当4=1+3时,x+y+z=13或x+y+z=31(舍),
∵x<y<z,
∴满足条件的M为139,148,157,238,247,256,346,
当4=2+2时,x+y+z=22,
∵x<y<z,
∴满足条件的M为589,678,
综上所述,所有满足条件的M为139,148,157,238,247,256,346,589,678.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】在矩形ABCD中,点P在AD上,AB=2,AP=1.直角尺的直角顶点放在点P处,直角尺的两边分别交AB、BC于点E、F,连接EF(如图1).
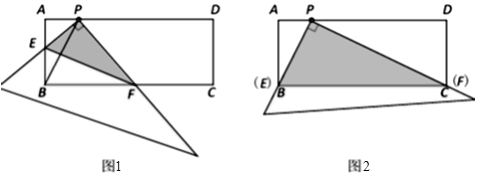
(1)当点E与点B重合时,点F恰好与点C重合(如图2).
①求证:△APB∽△DCP;
②求PC、BC的长.
(2)探究:将直角尺从图2中的位置开始,绕点P顺时针旋转,当点E和点A重合时停止.在这个过程中(图1是该过程的某个时刻),观察、猜想并解答:
① tan∠PEF的值是否发生变化?请说明理由.
② 设AE=x,当△PBF是等腰三角形时,请直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC的顶点A、B、C的坐标分别是A(-1,-1)、B(-4,-3)、C(-4,-1).
(1)将△ABC向右平移三个单位后得到![]() 则
则![]() _________;
_________;
(2)画出△ABC关于原点O中心对称的图形![]() .
.
(3)将△ABC绕原点A按顺时针方向旋转90°后得到![]() 画出
画出![]() 则
则![]() 的坐标为_________,
的坐标为_________,![]() 的坐标为_________.
的坐标为_________.

查看答案和解析>>
科目:初中数学 来源: 题型:
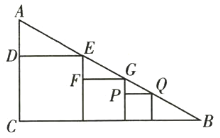
【题目】如图,在![]() 中,
中,![]() ,在
,在![]() 内有三个正方形,且这三个正方形都有一边在
内有三个正方形,且这三个正方形都有一边在![]() 上,都有一个顶点在
上,都有一个顶点在![]() 上,点
上,点![]() 在
在![]() 上,第一个正方形边
上,第一个正方形边![]() 长
长![]() ,第二个正方形边
,第二个正方形边![]() 长
长![]() ,那么第三个正方形的边
,那么第三个正方形的边![]() 长为______.
长为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
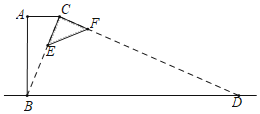
【题目】如图所示为某种型号的台灯的横截面图,已知台灯灯柱AB长30cm,且与水平桌面垂直,灯臂AC长为10cm,灯头的横截面△CEF为直角三角形,当灯臂AC与灯柱AB垂直时,沿CE边射出的光线刚好射到底座B点.若不考虑其它因素,则该台灯在桌面可照亮的宽度BD的长为_____cm.
查看答案和解析>>
科目:初中数学 来源: 题型:
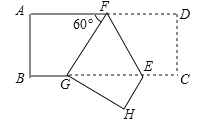
【题目】如图,在矩形ABCD中,点F在AD上,点E在BC上,把这个矩形沿EF折叠后,使点D恰好落在BC边上的G点处,若矩形面积为![]() 且∠AFG=60°,GE=2BG,则折痕EF的长为( )
且∠AFG=60°,GE=2BG,则折痕EF的长为( )
A. 1 B. ![]() C. 2 D.
C. 2 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=ax+1与x轴、y轴分别相交于A、B两点,与双曲线y=![]() (x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(x>0)相交于点P,PC⊥x轴于点C,且PC=2,点A的坐标为(﹣2,0).
(1)求双曲线的解析式;
(2)若点Q为双曲线上点P右侧的一点,且QH⊥x轴于H,当以点Q、C、H为顶点的三角形与△AOB相似时,求点Q的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某种商品每天的销售利润![]() (元)与销售单价
(元)与销售单价![]() (元)之间满足关系:
(元)之间满足关系:![]() ,其图像如图所示.
,其图像如图所示.
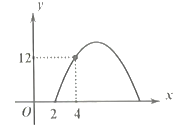
(1)销售单价为多少元时,这种商品每天的销售利润最大?最大利润为多少元?
(2)若该商品每天的销售利润不低于12元,则销售单价![]() 的取值范围是_____.
的取值范围是_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现有一块直角三角形的铁皮![]() ,
,![]() ,
,![]() ,
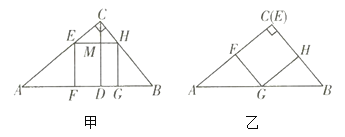
,![]() .要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
.要在其中剪出一个面积尽可能大的正方形,小红和小亮各想出了甲、乙两种方案,请你帮忙算一算哪一种方案剪出的正方形面积较大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com