
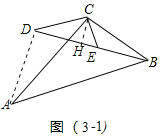
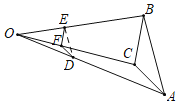
����Ŀ�����������֣���ͼ��1�����ڡ�OAB�͡�OCD�У�OA��OB��OC��OD����AOB����COD��45�㣬����AC��BD���ڵ�M��
��AC��BD֮���������ϵΪ�� ����
����AMB�Ķ���Ϊ�� ����
�����̽������ͼ��2�����ڡ�OAB�͡�OCD�У���AOB����COD��90�㣬��OAB����OCD��30�㣬����AC����BD���ӳ����ڵ�M�������![]() ��ֵ����AMB�Ķ�����
��ֵ����AMB�Ķ�����
��ʵ��Ӧ�ã���ͼ��3������һ��������������30��ǵĴ�С��ͬ��ֱ�����ǰ�ABC��DCE��ɵ�ͼ�Σ����С�ACB����DCE��90�㣬��A����D��30����D��E��B��ͬһֱ���ϣ�CE��1��BC��![]() �����A��D֮��ľ��룮
�����A��D֮��ľ��룮

���𰸡����������֡���AC=BD������AMB=45�㣻�����̽����![]() ����AMB=90�㣻��ʵ��Ӧ�á�4
����AMB=90�㣻��ʵ��Ӧ�á�4![]() ��5
��5![]()
��������
��������:��ͼ��1����֤����COA�ա�DOB��SAS�������ɽ�����⣮
���̽��:��ͼ��2����֤����COA�ס�ODB���ɵ�![]() ����MAK����OBK���ѽ���ɽ�����⣮
����MAK����OBK���ѽ���ɽ�����⣮
ʵ��Ӧ��:���������ν�ֱ�����������BE�����������������ε����ʽ�����⼴�ɣ�
�⣺��������:��ͼ��1���У���OA��BD��K��

�ߡ�AOB����COD��45����
���COA����DOB��
��OA��OB��OC��OD��
���COA�ա�DOB��SAS����
��AC��DB����CAO����DBO��
�ߡ�MKA����BKO��
���AMK����BOK��45����
�ʴ�Ϊ��AC��BD����AMB��45��
���̽��:��ͼ��2���У�

����OAB����OCD�У��ߡ�AOB����COD��90������OAB����OCD��30����
���COA����DOB��OC��![]() OD��OA��
OD��OA��![]() OB��
OB��
��![]() ��
��
���COA�ס�ODB��
��![]() ����MAK����OBK��
����MAK����OBK��
�ߡ�AKM����BKO��
���AMK����BOK��90����
ʵ��Ӧ��:��ͼ3��1�У���CH��BD��H������AD��
��Rt��DCE�У��ߡ�DCE��90������CDE��30����EC��1��
���CEH��60����
�ߡ�CHE��90����
���HCE��30����
��EH��![]() EC��
EC��![]() ��
��
��CH��![]() ��
��
��Rt��BCH��BH�� ��
��
��BE��BH��EH��4��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��4![]() ��
��
��ͼ3��2�У�����AD���� CH��DE��H��

ͬ���ɵ�BH��![]() ��EH��
��EH��![]() ��
��
��BE��![]() +
+![]() ��5��
��5��
�ߡ�DCA�ס�ECB��
��AD��BE��CD��EC��![]() ��
��
��AD��5![]() ��
��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �ı�
�ı�![]() ��
�� ![]() ��
�� ![]() ��
��![]() ��һ�㣬
��һ�㣬 ![]() ��
�� ![]() ��
��![]() ����һ���㣬������
����һ���㣬������![]() ��ֱ��
��ֱ��![]() �۵���
�۵��� ![]() �Ķ�Ӧ��Ϊ
�Ķ�Ӧ��Ϊ![]() ����
����![]() �ij�����Сʱ��
�ij�����Сʱ�� ![]() �ij�Ϊ__________��
�ij�Ϊ__________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
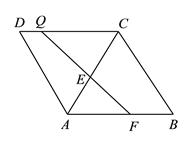
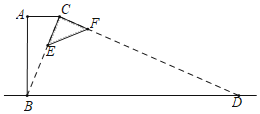
����Ŀ���ڡ�ABC�У�AB=BC=2����ABC=120��������ABC�Ƶ�B˳ʱ����ת������0�㣼����90�����á�A1BC1��A1B��AC�ڵ�E��A1C1�ֱ�AC��BC��D��F���㣮
��1����ͼ1���۲첢���룬����ת�����У��߶�BE��BF��������������ϵ����֤����Ľ��ۣ�
��2����ͼ2������=30��ʱ�����ж��ı���BC1DA����״����˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC�Ķ���A��B��C������ֱ���A(-1,-1)��B(-4,-3)��C(-4,-1).
(1)����ABC����ƽ��������λ��õ�![]() ��
��![]() _________��
_________��
(2)������ABC����ԭ��O���ĶԳƵ�ͼ��![]() .
.
(3)����ABC��ԭ��A��˳ʱ�뷽����ת90���õ�![]() ����
����![]() ��
��![]() ������Ϊ_________��
������Ϊ_________��![]() ������Ϊ_________.
������Ϊ_________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��ABC����ȡһ��O����AO��BO��CO���ֱ�ȡ��D��E��F��ʹOD��![]() AO��OE��
AO��OE��![]() BO��OF��
BO��OF��![]() CO������DEF��������˵����
CO������DEF��������˵����
����ABC����DEF��λ��ͼ�Σ�����ABC����DEF������ͼ�Σ�
����DEF����ABC���ܳ���Ϊ1��3������DEF����ABC�������Ϊ1��6��
����ȷ�ĸ����ǣ�������
A.1B.2C.3D.4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
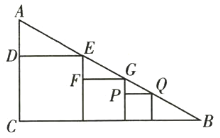
����Ŀ����ͼ����![]() �У�
��![]() ����
����![]() �������������Σ��������������ζ���һ����
�������������Σ��������������ζ���һ����![]() �ϣ�����һ��������
�ϣ�����һ��������![]() �ϣ���
�ϣ���![]() ��
��![]() �ϣ���һ�������α�
�ϣ���һ�������α�![]() ��
��![]() ���ڶ��������α�
���ڶ��������α�![]() ��
��![]() ����ô�����������εı�
����ô�����������εı�![]() ��Ϊ______.
��Ϊ______.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ʾΪij���ͺŵ�̨�Ƶĺ����ͼ����̨֪�Ƶ���AB��30cm������ˮƽ���洹ֱ���Ʊ�AC��Ϊ10cm����ͷ�ĺ�����CEFΪֱ�������Σ����Ʊ�AC�����AB��ֱʱ����CE������Ĺ��߸պ��䵽����B�㣮���������������أ����̨��������������Ŀ���BD�ij�Ϊ_____cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��y=ax+1��x�ᡢy��ֱ��ཻ��A��B���㣬��˫����y=![]() ��x��0���ཻ�ڵ�P��PC��x���ڵ�C����PC=2����A������Ϊ����2��0����
��x��0���ཻ�ڵ�P��PC��x���ڵ�C����PC=2����A������Ϊ����2��0����
��1����˫���ߵĽ���ʽ��
��2������QΪ˫�����ϵ�P�Ҳ��һ�㣬��QH��x����H�����Ե�Q��C��HΪ���������������AOB����ʱ�����Q�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������OABC�Ķ���O������ԭ��������A��x��������B��120�㣬OA��2��������OABC��ԭ��˳ʱ����ת105����OA��B��C����λ�������B��������Ϊ��������

A. ��![]() ��
��![]() �� B. ��
�� B. ��![]() ��
��![]() �� C. ��2����2�� D. ��
�� C. ��2����2�� D. ��![]() ��
��![]() ��
��
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com