[题目]如图.已知四边形ABCD是梯形.AB∥CD.AB＝BC＝DA＝1.CD＝2.按图中所示的规律.用2009个这样的梯形镶嵌而成的四边形的周长是．题目和参考答案——青夏教育精英家教网—

精英家教网 > 初中数学 > 题目详情

【题目】如图，已知四边形ABCD是梯形，AB∥CD，AB＝BC＝DA＝1，CD＝2，按图中所示的规律，用2009个这样的梯形镶嵌而成的四边形的周长是_____．

【答案】6029．

【解析】

本题的关键是从图片中找出规律，找出当n等于1、2、3、4…等时，的周长，从中找出它们的规律，依此来计算当n＝2009时的周长．

解：由图片知：

当n＝1时，即有1个这样的梯形组成的四边形的周长为：5

当n＝2时，即有2个这样的梯形组成的四边形的周长为：5+5﹣2

当n＝3时，即有3个这样的梯形组成的四边形的周长为：5+5﹣2+5﹣2

…

当n＝2009时，即有2009个这样的梯形组成的四边形的周长为：5+2008×（5﹣2）＝6029

故答案为:6029．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：初中数学 来源： 题型：

【题目】在正方形ABCD中，AB=8，点P在边CD上，tan∠PBC=，点Q是在射线BP上的一个动点，过点Q作AB的平行线交射线AD于点M，点R在射线AD上，使RQ始终与直线BP垂直．

（1）如图1，当点R与点D重合时，求PQ的长；

（2）如图2，试探索：的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；

（3）如图3，若点Q在线段BP上，设PQ=x，RM=y，求y关于x的函数关系式，并写出它的定义域．

查看答案和解析>>

科目：初中数学 来源： 题型：

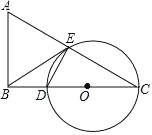
【题目】如图，在△ABC 中，∠ABC＝90°，∠C＝30°，AC 的垂直平分线交 BC 于点 D，交AC 于点 E．

(1)判断 BE 与△DCE 的外接圆⊙O 的位置关系，并说明理由；

(2)若 BE＝，BD＝1，求△DCE 的外接圆⊙O 的直径．

查看答案和解析>>

科目：初中数学 来源： 题型：

（1）如图1，当点R与点D重合时，求PQ的长；

（2）如图2，试探索：的比值是否随点Q的运动而发生变化？若有变化，请说明你的理由；若没有变化，请求出它的比值；

（3）如图3，若点Q在线段BP上，设PQ=x，RM=y，求y关于x的函数关系式，并写出它的定义域．

查看答案和解析>>

科目：初中数学 来源： 题型：

【题目】某镇道路改造工程，由甲、乙两工程队合作20天可完成．甲工程队单独施工比乙工程队单独施工多用30天完成此项工程．

（1）求甲、乙两工程队单独完成此项工程各需要多少天？

（2）若甲工程队独做a天后，再由甲、乙两工程队合作天（用含a的代数式表示）可完成此项工程；

（3）如果甲工程队施工每天需付施工费1万元，乙工程队施工每天需付施工费2.5万元，甲工程队至少要单独施工多少天后，再由甲、乙两工程队合作施工完成剩下的工程，才能使施工费不超过64万元？

查看答案和解析>>

科目：初中数学 来源： 题型：

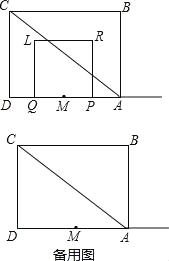
【题目】如图，四边形ABCD为矩形，AC为对角线，AB=6，BC=8，点M是AD的中点，P、Q两点同时从点M出发，点P沿射线MA向右运动；点Q沿线段MD先向左运动至点D后，再向右运动到点M停止，点P随之停止运动．P、Q两点运动的速度均为每秒1个单位．以PQ为一边向上作正方形PRLQ．设点P的运动时间为t（秒），正方形PRLQ与△ABC重叠部分的面积为S．

（1）当点R在线段AC上时，求出t的值．

（2）求出S与t之间的函数关系式，并直接写出取值范围．（求函数关系式时，只须写出重叠部分为三角形时的详细过程，其余情况直接写出函数关系式．）

（3）在点P、点Q运动的同时，有一点E以每秒1个单位的速度从C向B运动，当t为何值时，△LRE是等腰三角形．请直接写出t的值或取值范围．