
【题目】如图,数轴上有三个点A,B,C,请回答下列问题:
(1)将点C向左移动6个单位长度后,这时点B所表示的数比点C所表示的数大
多少?
(2)怎样移动A,B,C中的两个点,才能使这三个点表示相同的数?有几种移法?
![]()
【答案】(1)1;(2) 移动方法见解析,共有3种移法.
【解析】
(1)由图可知点B表示的数是-2,将点C向左移动6个单位长度后表示的数是-3,由此即可得到所求答案了;
(2)根据题意分以下三种情况结合已知条件解答即可:①移动A、C两点到B;②移动A、B两点到C;③移动B、C两点到A;
(1)∵点C原来表示的数是3,
∴将点C向左移动6个单位长度后所表示的新数是:3-6=-3,
又∵点B表示的数是-2,
∴点B表示的数比点C移动后表示的数大:-2-(-3)=-2+3=1;
(2)有3种移法.
①点A右移2个单位长度,点C左移5个单位长度;
②点A右移7个单位长度,点B右移5个单位长度;
③点B左移2个单位长度,点C左移7个单位长度.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1、O2、O3,…组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2015秒时,点P的坐标是( )
个单位长度,则第2015秒时,点P的坐标是( )
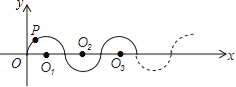
A. (2014,0) B. (2015,﹣1) C. (2015,1) D. (2016,0)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级学生开展踢毽子比赛活动,每班派5名学生参加.按团体总分多少排列名次.在规定时间每人踢100个以上(含100个)为优秀,下表是成绩最好的甲班和乙班5名学生的比赛数据(单位:个)

请你回答下列问题:
(1)填写表格;
(2)根据以上信息,请你回答下列问题:
①从平均数、众数相结合的角度分析,应该把冠军奖状发给哪一个班级?
②从优秀率的角度分析,应该把冠军奖状发给哪一个班级?
(3)如果两个班各选两名同学参加市踢毽子的比赛,你认为哪个班级团体实力更强?为什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数的图象经过点(0,﹣3),顶点坐标为(﹣1,﹣4),
(1)求这个二次函数的解析式;
(2)求图象与x轴交点A、B两点的坐标;
(3)图象与y轴交点为点C,求三角形ABC的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y=![]() (k为常数).
(k为常数).
(1)k为何值时,该函数是正比例函数;
(2)k为何值时,正比例函数过第一、三象限,写出正比例函数解析式;
(3)k为何值时,正比例函数y随x的增大而减小,写出正比例函数的解析式.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形). 
(1)将△ABC沿x轴方向向左平移6个单位,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2 , 并直接写出点B2、C2的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点M为直线AB上一动点, ![]() 都是等边三角形,连接BN
都是等边三角形,连接BN
![]() 求证:
求证: ![]() ;
;
![]() 分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系
分别写出点M在如图2和图3所示位置时,线段AB、BM、BN三者之间的数量关系![]() 不需证明
不需证明![]() ;
;
![]() 如图4,当
如图4,当![]() 时,证明:
时,证明: ![]() .
.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市规定:凡一次购买大米160kg以上可以按原价打折出售,购买160kg(包括160kg)以下只能按原价出售.小明家到超市买大米,原计划买的大米,只能按原价付款,需要600元;若多买40kg,则按打折价格付款,恰巧需要也是600元.
(1)求小明家原计划购买大米数量x(千克)的范围;
(2)若按原价购买4kg与打折价购买5kg的款相同,那么原计划小明家购买多少大米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们知道,任意一个正整数n都可以进行这样的分解:n=p×q(p,q是正整数,且p≤q),在n的所有这种分解中,如果p,q两因数之差的绝对值最小,我们就称p×q是n的最佳分解,并规定:F(n)=![]() ,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=
,例如12可以分解成1×12,2×6或3×4,因为12-1>6-2>4-3,所有3×4是最佳分解,所以F(12)=![]() .
.
(1)如果一个正整数a是另外一个正整数b的平方,我们称正整数a是完全平方数,求证:对任意一个完全平方数m,总有F(m)=1.
(2)如果一个两位正整数t,t=10x+y(1≤x≤y≤9,x,y为自然数),交换其个位上的数与十位上的数得到的新数减去原来的两位正整数所得的差为18,那么我们称这个数t为“吉祥数”,求所有“吉祥数”中F(t)的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com