练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

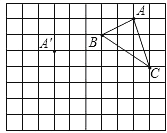
    【题目】△ABC的三个顶点的位置如图所示，现将△ABC平移，使点A变换为点A1，点B1、C1分别是B、C的对应点．

    （1）请画出平移后的△A1B1C1（不写画法）；

    （2）将△A1B1C1绕点C1顺时针旋转90°，画出旋转后的△A2B2C1（不写画法）

    【答案】（1）见解析；（2）见解析.

    【解析】

    （1）由图可判断出△ABC向下平移了2格，又向左平移了5格，由此确定B1、C1，画出图形即可；

    （2）根据绕点C1顺时针旋转90°，先确定C1A2、C1B2，再连接A2B2即可.

    解：（1）由图可知，△ABC先向下平移了2格，又向左平移了5格，按此平移规律将点B、C分别平移到点B1、C1，如图所示，连接A1B1、B1C1、A1C1，则△A1B1C1即为所求；

    （2）先将C1A1、C1B1绕点C1顺时针旋转90°得到C1A2、C1B2，如图所示，再连接A2B2，则△A2B2C1即为所求.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】已知，在△ABC中，∠A＝90°，AB＝AC，点D为BC的中点．

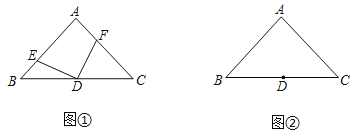
    （1）如图①，若点E、F分别为AB、AC上的点，且DE⊥DF．

    ①求证：BE＝AF；

    ②若S△BDE＝S△ABC＝2，求S△CDF；

    （2）若点E、F分别为AB、CA延长线上的点，且DE⊥DF．

    ①BE＝AF还成立吗？请利用图②说明理由；

    ②若S△BDE＝S△ABC＝8，直接写出DF的长.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】综合与探究

    如图1所示，直线y=x+c与x轴交于点A（﹣4，0），与y轴交于点C，抛物线y=﹣x2+bx+c经过点A，C．

    （1）求抛物线的解析式

    （2）点E在抛物线的对称轴上，求CE+OE的最小值；

    （3）如图2所示，M是线段OA的上一个动点，过点M垂直于x轴的直线与直线AC和抛物线分别交于点P、N

    ①若以C，P，N为顶点的三角形与△APM相似，则△CPN的面积为　 　；

    ②若点P恰好是线段MN的中点，点F是直线AC上一个动点，在坐标平面内是否存在点D，使以点D，F，P，M为顶点的四边形是菱形？若存在，请直接写出点D的坐标；若不存在，请说明理由．

    注：二次函数y=ax2+bx+c（a≠0）的顶点坐标为（﹣，）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

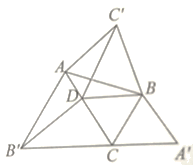
    【题目】如图所示，在△ABC中，已知∠DBC＝60°，AC＞BC，又△ABC＇、△BCA＇、△CAB＇都是△ABC形外的等边三角形，而点D在AC上，且BC＝DC

    (1)证明:△C＇BD≌△B＇DC

    (2)证明:△AC＇D≌△DB＇A

    查看答案和解析>>

    科目：初中数学 来源： 题型：

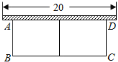
    【题目】如图，有长为的篱笆，一面利用墙（墙的最大可用长度为），围成中间隔有一道篱笆（平行于）的矩形花圃．设花圃的一边为．

    则________（用含的代数式表示），矩形的面积________（用含的代数式表示）；

    如果要围成面积为的花圃，的长是多少？

    将中表示矩形的面积的代数式通过配方，问：当等于多少时，能够使矩形花圃面积最大，最大的面积为多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图所示，在四边形ABDC中，∠A＝90°，AB＝9，AC＝12，BD＝8，CD＝17.

    (1)连接BC，求BC的长；

    (2)求四边形ABDC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知：如图，BE是△ABC的外接圆O的直径，CD是△ABC的高．

    （1）求证：AC·BC＝BE·CD；

    （2）已知CD＝6、AD＝3、BD＝8，求⊙O的直径BE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】中，，，将绕点按顺时针旋转得到，连接，，它们交于点，

    ①求证：．

    ②当，求的度数．

    ③当四边形是菱形时，求的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在中，，点是、平分线的交点，且，，则点到边的距离为（ ）

    A.B.C.D.

    查看答案和解析>>

    同步练习册答案