
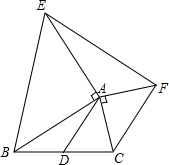
 已知,如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形(其中∠BAE=∠CAF=90°,AE=AB,AC=AF),求证:EF=2AD.
已知,如图,在△ABC中,AD是BC边上的中线,分别以AB,AC为直角边向外作等腰直角三角形(其中∠BAE=∠CAF=90°,AE=AB,AC=AF),求证:EF=2AD. 分析 延长AD到G,使DG=AD,连接BG,CG(如图),根据对角线互相平分的四边形是平行四边形,得到ABGC为平行四边形,然后根据平行四边形的性质得到CB=AC=AE,∠BAC+∠ABG=180°,再由已知∠BAC+∠FAE=180°,从而得到∠DAE=∠ABG,再由已知的等腰直角三角形ABD得到AB=AE,利用SAS求证△AEF≌△ABG,最后根据全等三角形的对应边相等即可得证.
解答 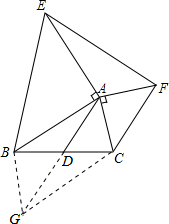 证明:延长AD到G,使DG=AD,连接BG,CG(如图)
证明:延长AD到G,使DG=AD,连接BG,CG(如图)
∵BD=CD,AD=DG,
∴四边形ABGC为平行四边形.
∴GB=AC=AF,∠BAC+∠ABF=180°
又∵∠BAC+∠FAE=180°,
∴∠DAE=∠ABG,
在△AEF与△ABG中,
$\left\{\begin{array}{l}{AB=AC}\\{∠ABG=∠EAF}\\{BG=AF}\end{array}\right.$,
∴△AEF≌△ABG(SAS),
∴EF=AG=2AD.
点评 本题考查了全等三角形的判定和性质,等腰直角三角形的性质,正确的作出辅助线是解题的关键.


科目:初中数学 来源: 题型:解答题
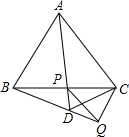 已知△ABC是边长为5的等边三角形.
已知△ABC是边长为5的等边三角形.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
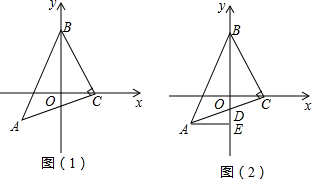
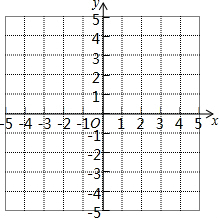 如图是建有平面直角坐标系的正方形网格,请按下列要求操作:
如图是建有平面直角坐标系的正方形网格,请按下列要求操作:查看答案和解析>>
科目:初中数学 来源:2016-2017学年浙江省瑞安市五校联考八年级下学期第一次月考数学试卷(解析版) 题型:解答题
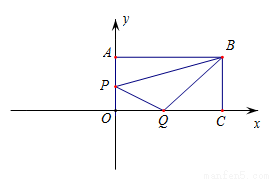
如图,长方形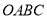 的边
的边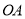 ,
, 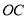 在坐标轴上,
在坐标轴上, 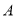 (0,2),
(0,2),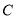 (4,0).点
(4,0).点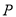 从点
从点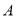 出发,以每秒1个单位长度的速度沿射线
出发,以每秒1个单位长度的速度沿射线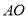 方向运动,同时点
方向运动,同时点 从点
从点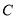 出发,以每秒2个单位的速度沿射线
出发,以每秒2个单位的速度沿射线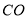 方向运动.设点
方向运动.设点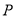 运动时间为
运动时间为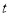 秒(
秒(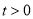 ).
).
(1)当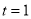 时,求△
时,求△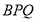 的周长;
的周长;
(2)当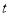 为何值时,△
为何值时,△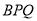 是等腰三角形;
是等腰三角形;
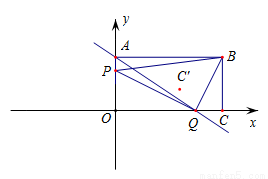
(3)点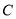 关于
关于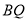 的对称点为
的对称点为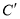 ,当
,当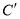 恰好落在直线
恰好落在直线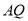 上时,△
上时,△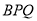 的面积为__________.(直接写出结果)
的面积为__________.(直接写出结果)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com