
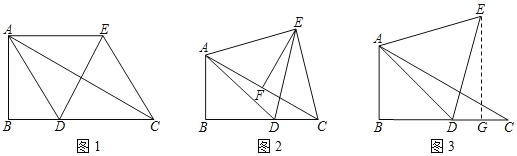
【题目】已知:在Rt△ABC中,∠B=90°,∠ACB=30°,点D为BC边上一动点,以AD为边,在AD的右侧作等边三角形ADE.
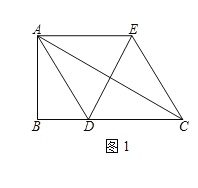
(1)当AD平分∠BAC时,如图1,四边形ADCE是 形;
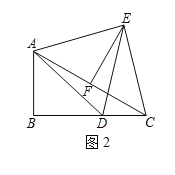
(2)过E作EF⊥AC于F,如图2,求证:F为AC的中点;
(3)若AB=2,
①当D为BC的中点时,过点E作EG⊥BC于G,如图3,求EG的长;
②点D从B点运动到C点,则点E所经过路径长为 .(直接写出结果)
【答案】(1)菱形;(2)证明见解析;(3)①EG![]() ;②2
;②2![]() .
.
【解析】
(1)根据平行四边形的判定定理得到四边形ADCE为平行四边形,证明AD=AE,根据菱形的判定定理证明结论;
(2)证明△BAD≌△FAE,根据全等三角形的性质得到AB=AF,根据直角三角形的性质得到AC=2AB,证明结论;
(3)①作EF⊥AC于F,连接EC,根据勾股定理求出BC,根据等腰三角形的性质求出CG,根据勾股定理计算,得到答案; ②根据线段垂直平分线的判定定理得到E'E'垂直平分AC,证明△E'AE'≌△BAC,得到E'E'=BC=![]() .
.
解:(1)在Rt△ABC中,∠B=90°,∠ACB=30°,
∴∠BAC=60°.
∵AD平分∠BAC,
∴∠BAD=∠DAC=30°.
∵△ADE为等边三角形,
∴∠DAE=60°,
∴∠EAC=30°,
∴∠EAC=∠ACB,∠DAC=∠ACB,
∴AE∥DC,AD=DC.
∵AE=AD,∴AE=CD,
∴四边形ADCE为平行四边形.
∵AD=AE,
∴平行四边形ADCE为菱形.
故答案为:菱形;
(2)![]()
![]()
在△BAD和△FAE中,
 ,
,
∴△BAD≌△FAE(AAS),
∴AB=AF,
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB,
∴AC=2AF,
∴F为AC的中点;
(3)①如图3,作EF⊥AC于F,连接EC,
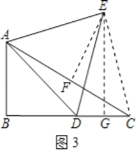
在Rt△ABC中,∠B=90°,∠ACB=30°,
∴AC=2AB=4,
∴BC![]() 2
2![]() ,
,
∵D为BC的中点,
∴BD![]() BC
BC![]() ,
,
∴AD![]() ,
,
∵AF=FC,EF⊥AC,
∴EC=AE=AD![]() ,
,
∵EC=EA=ED,EG⊥DC,
∴CG![]() CD
CD![]() ,
,
∴EG![]() ;
;
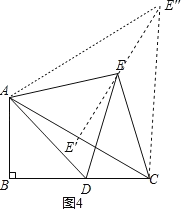
②如图4,当点D与点B重合时,点E在E'处,点E'是AC中点;
当点D与点C重合时,点E在E'处,其中△ACE'是等边三角形,
由(1)得:AE=CE,∴点E始终落在线段AC的垂直平分线上,
∴E'E'垂直平分AC,
∴点E的运动路径是从AC的中点E',沿着AC垂直平分线运动到E'处,
在△E'AE'和△BAC中,
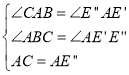 ,
,
∴△E'AE'≌△BAC(AAS),
∴E'E'=BC=2![]() .
.
故答案为:2![]() .
.


科目:初中数学 来源: 题型:
【题目】某学校为了了解在校初中生阅读数学文化史类书籍的现状,随机抽取了初中部部分学生进行研究调查,依据相关数据绘制成以下不完整的的统计图表,请你根据图表中的信息解答下列问题:
类别 | 人数 | 占总人数比例 |
重视 | a | 0.3 |
一般 | 57 | 0.38 |
不重视 | b | C |
说不清楚 | 9 | 0.06 |
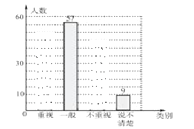
(1)求表格中a,b,c的值,并补全统计图;
(2)若该校共有初中生2400名,请估计该校“不重视”阅读数学文化史书籍的初中生人数;
(3)若小明和小华去书店,打算从A,B,C,D四本数学文化史类书籍中随机选取一本,请用画树状图或列表格的方法,求两人恰好选中同一本书籍的概率。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:由两条与x轴有着相同的交点,并且开口方向相同的抛物线所围成的封闭曲线称为“月牙线”.如图,抛物线C1与抛物线C2组成一个开口向上的“月牙线”,抛物线C1与抛物线C2与x轴有相同的交点M,N(点M在点N的左侧),与y轴的交点分别为A,B且点A的坐标为(0,﹣3),抛物线C2的解析式为y=mx2+4mx﹣12m,(m>0).
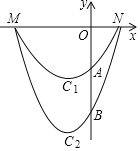
(1)请你根据“月牙线”的定义,设计一个开口向下.“月牙线”,直接写出两条抛物线的解析式;
(2)求M,N两点的坐标;
(3)在第三象限内的抛物线C1上是否存在一点P,使得△PAM的面积最大?若存在,求出△PAM的面积的最大值;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2018郑州模拟)冬季即将来临,某电器超市销售每台进价分别为300元、255元的A,B两种型号的电热扇,下表是近两周的销售情况:
销售时段 | |||
销售数量 | |||
A种型号 | B种型号 | 销售收入 | |
第一周 | 2台 | 3台 | 1695元 |
第二周 | 5台 | 6台 | 3765元 |
(进价、售价均保持不变,利润![]() 销售收入
销售收入![]() 进货成本)
进货成本)
(1)分别求出A,B两种型号电热扇的销售单价;
(2)若超市准备用不超过8100元的金额再采购这两种型号的电热扇共30台,求A种型号的电热扇最多能采购多少台?
(3)在(2)的条件下,超市销售完这30台电热扇能否实现利润为2100元的目标?若能,请给出相应的采购方案;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】复课返校后,为了让同学们进一步了解“新型冠状病毒”的防控知识,某学校组织了一次关于“新型冠状病毒”的防控知识比赛,从问卷中随机抽查了一部分,对调查结果进行了分组统计,并制作了表格与条形统计图(如图):
分组结果 | 频数 | 频率 |
| 30 | 0.3 |
| 50 |
|
|
| 0.15 |
| 5 |
|

请根据上图完成下面题目:
(1)总人数为 人,![]() ,
,![]() .
.
(2)请求出n的值并补全条形统计图.
(3)若全校有2700人,请你估算一下全校对“新型冠状病毒”的防控知识“完全掌握”的人数有多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】事业单位人员编制连进必考,现一事业单位需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方而进行量化考核.甲、乙、丙各项得分如下表:
笔试 | 面试 | 体能 | |
甲 | 84 | 80 | 88 |
乙 | 94 | 92 | 69 |
丙 | 81 | 84 | 78 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序;
(2)该单位规定:笔试、面试、体能分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分.根据规定,请你说明谁将被录用.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AB=![]() ,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为______.
,AC=5,tanA=2,D是BC中点,点P是AC上一个动点,将△BPD沿PD折叠,折叠后的三角形与△PBC的重合部分面积恰好等于△BPD面积的一半,则AP的长为______.

查看答案和解析>>
科目:初中数学 来源: 题型:
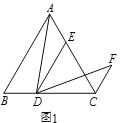
【题目】(1)问题发现:如图1,在等边![]() 中,点
中,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() 得到
得到![]() ,连接
,连接![]() .则
.则![]() 与
与![]() 的数量关系是_____,
的数量关系是_____,![]() 的度数为______.
的度数为______.
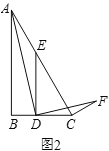
(2)拓展探究:如图2,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 为
为![]() 边上一动点,
边上一动点,![]() 交
交![]() 于点
于点![]() ,当∠ADF=∠ACF=90°时,求
,当∠ADF=∠ACF=90°时,求![]() 的值.
的值.
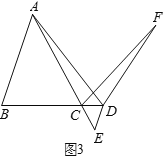
(3)解决问题:如图3,在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 的延长线上一点,过点
的延长线上一点,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() ,直接写出当
,直接写出当![]() 时
时![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com