
【题目】商场某种商品平均每天可销售30件,每件盈利50元,为了尽快减少库存,商场决定采取适当降价的措施.经调查发现:每件商品每降价1元,商场平均每天可多售出2件.设每件商品降价![]() 元.
元.
(1)商场日销售量为_____________件,每件商品盈利_______________元(用含![]() 的代数式表示)
的代数式表示)
(2)根据上述条件,每件商品降价多少元时,商场日盈利可达到2100元.
科目:初中数学 来源: 题型:
【题目】关于x的一元二次方程(2m+1)x2+4mx+2m﹣3=0
(Ⅰ)当m=![]() 时,求方程的实数根;
时,求方程的实数根;
(Ⅱ)若方程有两个不相等的实数根,求实数m的取值范围;
查看答案和解析>>
科目:初中数学 来源: 题型:
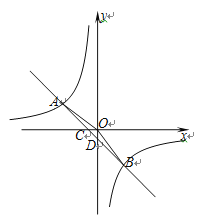
【题目】如图,在平面直角坐标系中,一次函数![]() 的图象与反比例函数
的图象与反比例函数![]() 的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=
的图象交于第二、四象限内的A,B两点,与x轴交于点C,与y轴交于点D,点B的坐标是(m,﹣4),连接AO,AO=5,sin∠AOC=![]() .
.
(1)求反比例函数的解析式
(2)连接OB,求△AOB的面积
(3) 根据图象直接写出当![]() 时,x的取值范围.
时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于一元二次方程ax2+bx+c=0(a≠0),下列说法:①a+c=0,方程ax2+bx+c=0,有两个不相等的实数;②若方程ax2+bx+c=0有两个不相等的实根.则方程cx2+bx+a=0也一定有两个不相等的实根;③若c是方程ax2+bx+c=0的一个根,则一定有ac+b+1=0成立;④若m是方程ax2+bx+c=0的一个根,则一定有b2-4ac=(2am+b)2成立,其中正确的结论是_____.(把你认为正确结论的序号都填上)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (
(![]() )的
)的![]() 与
与![]() 的部分对应值如下表.则下列判断中正确的是( )
的部分对应值如下表.则下列判断中正确的是( )
| … | -1 | 0 | 1 | 2 | … |
| … | -5 | 1 | 3 | 1 | … |
A.抛物线开口向上B.抛物线与![]() 轴交于负半轴
轴交于负半轴
C.当![]() 时,
时,![]() D.方程
D.方程![]() 的正根在2和3之间
的正根在2和3之间
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(10分)水果店张阿姨以每斤2元的价格购进某种水果若干斤,然后以每斤4元的价格出售,每天可售出100斤,通过调查发现,这种水果每斤的售价每降低0.1元,每天可多售出20斤,为保证每天至少售出260斤,张阿姨决定降价销售.
(1)若将这种水果每斤的售价降低x元,则每天的销售量是 斤(用含x的代数式表示);
(2)销售这种水果要想每天盈利300元,张阿姨需将每斤的售价降低多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,抛物线![]() 与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
与x轴交于A,B两点(A在B的左侧),与y轴交于点C,顶点为D.
(1)请直接写出点A,C,D的坐标;
(2)如图(1),在x轴上找一点E,使得△CDE的周长最小,求点E的坐标;
(3)如图(2),F为直线AC上的动点,在抛物线上是否存在点P,使得△AFP为等腰直角三角形?若存在,求出点P的坐标,若不存在,请说明理由.
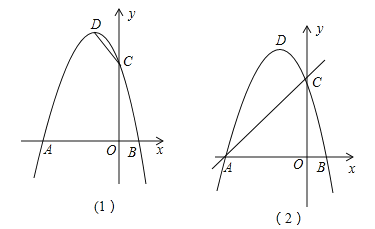
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面坐标系xOy中,点A的坐标为(1,0),点P的横坐标为2,将点A绕点P旋转,使它的对应点B恰好落在x轴上(不与A点重合);再将点B绕点O逆时针旋转90°得到点C.

(1)直接写出点B和点C的坐标;
(2)求经过A,B,C三点的抛物线的表达式.
查看答案和解析>>
科目:初中数学 来源: 题型:
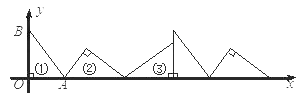
【题目】如图①,在△AOB 中,∠AOB=90,OA=3,OB=4.将△AOB 沿 x 轴依次以点 A、B、O为旋转中心顺时针旋转,分别得到图②图③、…,则旋转得到的图⑧的直角顶点的坐标为____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com