
【题目】如图,在△ABC中,E是AC边上的一点,且AE=AB,∠BAC=2∠CBE,以AB为直径作⊙O交AC于点D,交BE于点F.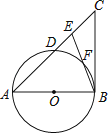
(1)求证:BC是⊙O的切线;
(2)若AB=8,BC=6,求DE的长.
【答案】
(1)
证明:∵AE=AB,
∴△ABE是等腰三角形,
∴∠ABE= ![]() (180°﹣∠BAC=)=90°﹣
(180°﹣∠BAC=)=90°﹣ ![]() ∠BAC,
∠BAC,
∵∠BAC=2∠CBE,
∴∠CBE= ![]() ∠BAC,
∠BAC,
∴∠ABC=∠ABE+∠CBE=(90°﹣ ![]() ∠BAC)+
∠BAC)+ ![]() ∠BAC=90°,
∠BAC=90°,
即AB⊥BC,
∴BC是⊙O的切线
(2)
解: 连接BD,
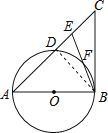
∵AB是⊙O的直径,
∴∠ADB=90°,
∵∠ABC=90°,
∴∠ADB=∠ABC,
∵∠A=∠A,
∴△ABD∽△ACB,
∴ ![]() ,
,
∵在Rt△ABC中,AB=8,BC=6,
∴AC= ![]() =10,
=10,
∴ ![]() ,
,
解得:AD=6.4,
∵AE=AB=8,
∴DE=AE﹣AD=8﹣6.4=1.6
【解析】(1)由AE=AB,可得∠ABE=90°﹣ ![]() ∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.此题考查了切线的判定与性质、相似三角形的判定与性质、等腰三角形的性质以及勾股定理.注意准确作出辅助线,证得△ABD∽△ACB是解此题的关键.
∠BAC,又由∠BAC=2∠CBE,可求得∠ABC=∠ABE+∠CBE=90°,继而证得结论;(2)首先连接BD,易证得△ABD∽△ACB,然后由相似三角形的对应边成比例,求得答案.此题考查了切线的判定与性质、相似三角形的判定与性质、等腰三角形的性质以及勾股定理.注意准确作出辅助线,证得△ABD∽△ACB是解此题的关键.
【考点精析】认真审题,首先需要了解等腰三角形的性质(等腰三角形的两个底角相等(简称:等边对等角)),还要掌握勾股定理的概念(直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2)的相关知识才是答题的关键.


科目:初中数学 来源: 题型:
【题目】在一次社会调查活动中,小华收集到某“健步走运动”团队中20名成员一天行走的步数,记录如下:
5640 | 6430 | 6520 | 6798 | 7325 |
8430 | 8215 | 7453 | 7446 | 6754 |
7638 | 6834 | 7326 | 6830 | 8648 |
8753 | 9450 | 9865 | 7290 | 7850 |
对这20个数据按组距1000进行分组,并统计整理,绘制了如下尚不完整的统计图表:
步数分组统计表
组别 | 步数分组 | 频数 |
A | 5500≤x<6500 | 2 |
B | 6500≤x<7500 | 10 |
C | 7500≤x<8500 | m |
D | 8500≤x<9500 | 3 |
E | 9500≤x<10500 | n |
请根据以上信息解答下列问题: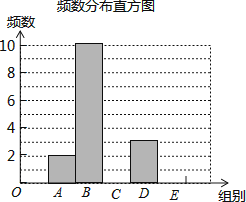
(1)填空:m= , n=
(2)补全频数发布直方图;
(3)这20名“健步走运动”团队成员一天行走步数的中位数落在组;
(4)若该团队共有120人,请估计其中一天行走步数不少于7500步的人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是某市一座人行天桥的示意图,天桥离地面的高BC是10米,坡面10米处有一建筑物HQ,为了方便使行人推车过天桥,市政府部门决定降低坡度,使新坡面DC的倾斜角∠BDC=30°,若新坡面下D处与建筑物之间需留下至少3米宽的人行道,问该建筑物是否需要拆除(计算最后结果保留一位小数).(参考数据: ![]() =1.414,
=1.414, ![]() =1.732)
=1.732)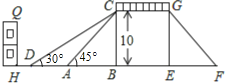
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数学课上,张老师举了下面的例题:
例1 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() )
)
例2 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.(答案:
的度数.(答案:![]() 或
或![]() 或
或![]() )
)
张老师启发同学们进行变式,小敏编了如下一题:
变式 等腰三角形![]() 中,
中,![]() ,求
,求![]() 的度数.
的度数.
(1)请你解答以上的变式题.
(2)解(1)后,小敏发现,![]() 的度数不同,得到
的度数不同,得到![]() 的度数的个数也可能不同.如果在等腰三角形
的度数的个数也可能不同.如果在等腰三角形![]() 中,设
中,设![]() ,当
,当![]() 有三个不同的度数时,请你探索
有三个不同的度数时,请你探索![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在四边形ABCD中,AD∥BC,DE⊥BC,垂足为点E,连接AC交DE于点F,点G为AF的中点,∠ACD=2∠ACB.若AF=50,EC=7,则DE的长为( )
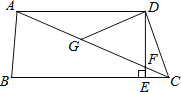
A. 14 B. 21 C. 24 D. 25
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB∥CD,以点A为圆心,小于AC长为半径作圆弧,分别交AB,AC于E,F两点,再分别以E,F为圆心,大于![]() EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。
EF长为半径作圆弧,两条圆弧交于点P,作射线AP,交CD于点M。

(1)若∠ACD=114°,求∠MAB的度数;
(2)若CN⊥AM,垂足为N,求证:△ACN≌△MCN。
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,平行四边形ABCD中,AB⊥AC,AB=1,BC= ![]() .对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F.
.对角线AC,BD相交于点O,将直线AC绕点O顺时针旋转,分别交BC,AD于点E,F. 
(1)证明:当旋转角为90°时,四边形ABEF是平行四边形;
(2)试说明在旋转过程中,线段AF与EC总保持相等;
(3)在旋转过程中,四边形BEDF可能是菱形吗?如果不能,请说明理由;如果能,说明理由并求出此时AC绕点O顺时针旋转的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com