
����Ŀ��ij��ѧΪ��Ԥ�ⱾУӦ���ҵŮ����һ������������Ŀ����������Ӿ��꼶�����ȡ����Ů�����и���Ŀ���ԣ����Բ�������Ϊ���������Ƴ���ͼ10��ʾ�IJ���Ƶ���ֲ�ֱ��ͼ�����������η�Ϊ����С�飬ÿС�麬��Сֵ���������ֵ��������ͳ��ͼ������ͳ��ͼ�ṩ����Ϣ����������⣺
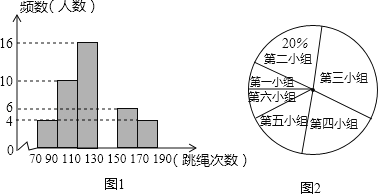
��1����ȫƵ���ֲ�ֱ��ͼ����ָ������������ݵ���λ�����ڵ� С�飻
��2�������Ծ��꼶Ů����һ��������������������130�εijɼ�Ϊ���㣬��У���꼶Ů������260�ˣ�����Ƹ�У���꼶Ů����һ�����������ɼ�Ϊ�����������
��3������Ծ��꼶Ů����һ��������������������170�εijɼ�Ϊ���֣�����������У��ӳɼ�Ϊ�����Ů������ѡһ�ˣ����ijɼ�Ϊ���ֵĸ����Ƕ��٣�
���𰸡���1����������2����104�ˣ���3����0.2
��������
�����������1�������ݵڶ�С��ռ��20%�����������Ȼ���������С�����������ȫƵ��ֱ��ͼ����2������������������ı���������⣻��3���������ֵ�������������������ɵó����ֵĸ��ʣ�
�����������1�����������ǣ�10��20%=50���ˣ��� �������������ǣ�50��4��10��16��6��4=10��
����λ��λ�ڵ����飻
��2������У���꼶Ů����һ�����������ɼ�Ϊ����������ǣ���50��4��10��16����50��260=104���ˣ���
��3�����ɼ�������������ǣ�10+6+4=20���ˣ��� �ɼ�Ϊ���ֵ�������4��
��ӳɼ�Ϊ�����Ů������ѡһ�ˣ����ijɼ�Ϊ���ֵĸ�����![]() =0.2��
=0.2��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪MB=ND,��MBA=��NDC�����������в����ж���ABM����CDN���ǣ� ��

A. ��M=��N B. AM=CN C. AB=CD D. AM��CN
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������з���ֽ�еġ�ABC����ƽ��7��������ƽ��2�õ���![]() ����1������ƽ�ƺ�������Σ�
����1������ƽ�ƺ�������Σ�
��2����AB=5����![]() = ��
= ��
��3������AA1,BB1, ���ݡ�ͼ��ƽ�ơ�������,�ã��߶�AA1���߶�BB1��������ϵ��λ�ù�ϵ��: ��
��4����ͼ����![]() AC+��
AC+��![]() BC�Ķ�����
BC�Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����������Ϊ������������ȥ��ɽ�羰�����Σ��Ƴ������µ��շѱ���

���ݸ���������֯Ա��ȥ��ɽ�羰�����Σ���֧����������������η���27 000Ԫ�����ʸõ�λ��ι��ж���Ա��ȥ��ɽ�羰�����Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ֱ��MN��ֱ��PQ��ֱ�ཻ��O����A������OP���˶�����B ������OM���˶�.
��1����ͼ1����֪AE��BE�ֱ��ǡ�BAO�͡�ABO�ǵ�ƽ���ߣ���A��B���˶��Ĺ����У���AEB�Ĵ�С�Ƿ�ᷢ���仯���������仯����˵���仯����������������仯���������AEB�Ĵ�С.
��2����ͼ2����֪AB��ƽ��CD��AD��BC�ֱ��ǡ�BAP�͡�ABM�Ľ�ƽ���ߣ�AD��BC���ӳ��߽��ڵ�F����A��B���˶��Ĺ����У���F= ����DE��CE�ֱַ��ǡ�ADC�͡�BCD�Ľ�ƽ���ߣ���A��B���˶��Ĺ����У���CED�Ĵ�СҲ�������仯�����СΪ��CED= ��.
��3����ͼ3���ӳ�BA��G����֪��BAO����OAG�Ľ�ƽ�������BOQ�Ľ�ƽ�������ӳ����ཻ��E��F�����EAF= �� ������AEF�У������һ��������һ���ǵ�3�������ABO= ��.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
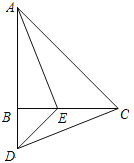
����Ŀ����ͼ������ABC�У�AB��CB����ABC��90�㣬DΪAB�ӳ�����һ�㣬��E��BC���ϣ���BE��BD������AE��DE��DC��
�� ��֤����ABE�ա�CBD��
�� ����CAE��30��������BDC�Ķ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס��������ۿ����72ǧ����һ���ִ��Ӽ۳�����˳������3Сʱ�����Ҹۣ���Ϣ1Сʱ���������أ�һ�ҿ�ͧ���ִ�����2Сʱ����Ҹ۳�������������2Сʱ���ۣ����������أ���ͷʱ����Բ��ƣ�����֪ˮ���ٶ���2ǧ��/ʱ����ͼ��ʾ�ִ��Ϳ�ͧ��۵ľ���y��ǧ�ף����ִ�����ʱ��x��Сʱ��֮��ĺ�����ϵʽ�����ͼ�����������⣺
��˳���ٶ�=���ھ�ˮ���ٶȣ�ˮ���ٶȣ������ٶ�=���ھ�ˮ���ٶȣ�ˮ���ٶȣ�

��1���ִ��ھ�ˮ�е��ٶ��� ǧ��/ʱ����ͧ�ھ�ˮ�е��ٶ��� ǧ��/ʱ��
��2�����ͧ����ʱ�Ľ���ʽ��д���Ա���ȡֵ��Χ��
��3����ͧ�����ʱ�䣬�ִ��Ϳ�ͧ�ڷ���;�����12ǧ������ֱ��д�������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У� ![]() �DZ߳�Ϊ
�DZ߳�Ϊ![]() �ĵȱ������Σ�ֱ��
�ĵȱ������Σ�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��
��![]() �ֱ��ڵ�
�ֱ��ڵ�![]() ��
��![]() ��
��![]() ��
�� ![]() ������
������![]() ��
��![]() ����
����![]() �ڵ�
�ڵ�![]() ��
��
��![]() ����
����![]() ������Ϊ__________��������������ţ�
������Ϊ__________��������������ţ�
��![]() ����֤����
����֤����![]() ��
��![]() ����
����![]() ��Գƣ�
��Գƣ�
��![]() ����
����![]() ����ֱ��
����ֱ��![]() ��Ӧ�ĺ�������ʽ��
��Ӧ�ĺ�������ʽ��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����3��0��-1��-2��-3��������У������ȡһ��������Ϊ����y=��5-m2��x����x�ķ��̣�m+1��x2+mx+1=0��m��ֵ��ǡ��ʹ���ú�����ͼ����һ�������ޣ��ҷ�����ʵ�����ĸ���Ϊ .
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com