
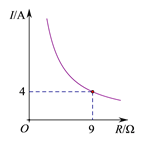
【题目】已知蓄电池的电压U为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)是反比例函数关系,它的图象如图所示.
(1)求这个反比例函数的表达式;
(2)如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器的可变电阻R应控制在什么范围?请根据图象,直接写出结果 .
科目:初中数学 来源: 题型:
【题目】如图,半径为1个单位的圆片上有一点A与数轴上的原点重合,AB是圆片的直径.(注:结果保留π )
(1)把圆片沿数轴向右滚动半周,点B到达数轴上点C的位置,点C表示的数是 数(填“无理”或“有理”),这个数是 ;
(2)把圆片沿数轴滚动2周,点A到达数轴上点D的位置,点D表示的数是 ;
(3)圆片在数轴上向右滚动的周数记为正数,圆片在数轴上向左滚动的周数记为负数,依次运动情况记录如下:+2,﹣1,+3,﹣4,﹣3.
①第 次滚动后,A点距离原点最近,第 次滚动后,A点距离原点最远.
②当圆片结束运动时,A点运动的路程共有 ,此时点A所表示的数是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】身高1.65米的兵兵在建筑物前放风筝,风筝不小心挂在了树上.在如图所示的平面图形中,矩形CDEF代表建筑物,兵兵位于建筑物前点B处,风筝挂在建筑物上方的树枝点G处(点G在FE的延长线上).经测量,兵兵与建筑物的距离BC=5米,建筑物底部宽FC=7米,风筝所在点G与建筑物顶点D及风筝线在手中的点A在同一条直线上,点A距地面的高度AB=1.4米,风筝线与水平线夹角为37°.
(1)求风筝距地面的高度GF;
(2)在建筑物后面有长5米的梯子MN,梯脚M在距墙3米处固定摆放,通过计算说明:若兵兵充分利用梯子和一根米长的竹竿能否触到挂在树上的风筝?
(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】
(1)在数轴上表示下列各数:0,–2.5,![]() ,–2,+5,
,–2,+5,![]() .
.
![]()
(2)将上列各数用“<”连接起来:___________ _____________________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是一个“有理数转换器”(箭头是数进入转换器的路径,方框是对进入的数进行转换的转换器)
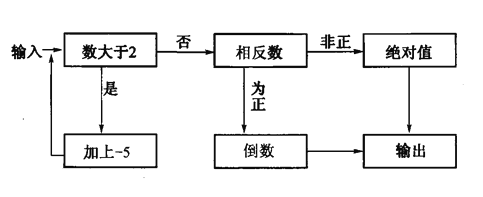
(1)当小明输入-3、![]() 、0.4这三个数时,三次输出的结果分别是 、_______、 .
、0.4这三个数时,三次输出的结果分别是 、_______、 .
(2)你认为当输入 时(写出2个即可),其输出结果是0?
(3)你认为这个“有理数转换器”不可能输出 数?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知关于x的一元二次方程x2﹣(k+1)x+2k﹣2=0.
(1)求证:此方程总有两个实数根;
(2)若此方程有一个根大于0且小于1,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
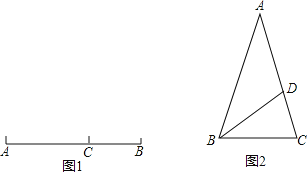
【题目】黄金分割具有严格的比例性、艺术性、和谐性,蕴藏着丰富的美学价值。黄金分割是指将整体一分为二,较大部分与整体部分的比值等于较小部分与较大部分的比值,其比值约为0.618。这个比值,被称为黄金分割数。我国著名数学家华罗庚普及并做出重要贡献的优选法中有一种0.618法也应用了黄金分割数。
定义:点C在线段AB上,若满足AC2=BCAB,则称点C为线段AB的黄金分割点(如图1).
如图2,△ABC中,AB=AC=1,∠A=36°,BD平分∠ABC交AC于点D.
(1)求证:点D是线段AC的黄金分割点;
(2)求出线段AD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com