
【题目】已知直线AB∥CD.
(1)如图1,直接写出∠ABE,∠CDE和∠BED之间的数量关系是 .
(2)如图2,BF,DF分别平分∠ABE,∠CDE,那么∠BFD和∠BED有怎样的数量关系?请说明理由.
(3)如图3,点E在直线BD的右侧,BF,DF仍平分∠ABE,∠CDE,请直接写出∠BFD和∠BED的数量关系 .

【答案】(1)∠ABE+∠CDE=∠BED;(2)详见解析;(3)2∠BFD+∠BED=360°.
【解析】试题分析:(1)点E作EF∥AB,根据平行线的性质易证得∠1=∠ABE,∠2=∠CDE,则可得∠ABE+∠CDE=∠BED;(2)∠BFD=![]() ∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED,已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠ABF+∠CDF=
∠CDE,所以∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=
(∠ABE+∠CDE),由(1)的结论可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=
(∠ABE+∠CDE),∠BED=∠ABE+∠CDE,所以∠BFD=![]() ∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=
∠BED;(3过点E作EG∥CD,根据平行公理可得AB∥CD∥EG,根据平行线的性质易证∠ABE+∠CDE+∠BED=360°,再由(1)的方法可得∠BFD=∠ABF+∠CDF;已知BF,DF分别平分∠ABE,∠CDE,根据角平分线的性质可得∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,所以∠BFD=
∠CDE,所以∠BFD=![]() (∠ABE+∠CDE),即2∠BFD+∠BED=360°.
(∠ABE+∠CDE),即2∠BFD+∠BED=360°.
试题解析:
(1)∠ABE+∠CDE=∠BED.
理由:如图1,作EF∥AB,
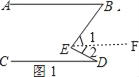
∵直线AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案为:∠ABE+∠CDE=∠BED.
(2)∠BFD=![]() ∠BED.
∠BED.
理由:如图2,∵BF,DF分别平分∠ABE,∠CDE,
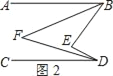
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1),可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
(3)2∠BFD+∠BED=360°.
理由:如图3,过点E作EG∥CD,
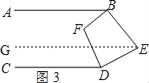
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分别平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案为:2∠BFD+∠BED=360°.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案科目:初中数学 来源: 题型:
【题目】列方程解应用题.
 程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
程大位,明代商人,珠算发明家,被称为珠算之父、卷尺之父.少年时,读书极为广博,对数学颇感兴趣,60岁时完成其杰作《直指算法统宗》(简称《算法统宗》).
在《算法统宗》里记载了一道趣题:一百馒头一百僧,大僧三个更无争,小僧三人分一个,大小和尚各几丁?意思是:有100个和尚分100个馒头,如果大和尚1人分3个,小和尚3人分1个,正好分完.试问大、小和尚各多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
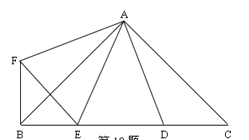
【题目】如图,∠BAC=∠DAF=90°,AB=AC,AD=AF,点D、E为BC边上的两点,且∠DAE=45°,连接EF、BF,则下列结论:①△AED≌△AEF ②△AED为等腰三角形
③BE+DC>DE④BE2+DC2=DE2,其中正确的有( )个
A. 4 B. 3 C. 2 D. 1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】有一列数,第一个数为x1=1,第二个数为x2=3,从第三个数开始依次为x3,x4,…,xn,….从第二个数开始,每个数是左右相邻两个数和的一半,如x2=![]() ,x3=
,x3=![]() .
.
(1)求x3,x4,x5的值,并写出计算过程;
(2)根据(1)的结果,推测x9等于多少;
(3)探索这一列数的规律,猜想第k(k为正整数)个数xk等于多少.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】Rt△ABC中,∠ACB=90°,BC=4,如图1,点P从C出发向点B运动,点R是射线PB上一点,PR=3CP,过点R作QR⊥BC,且QR=aCP,连接PQ,当P点到达B点时停止运动.设CP=x,△ABC与△PQR重合部分的面积为S,S关于x的函数图象如图2所示(其中0<x≤![]() ,
, ![]() <x≤m,m<x≤n时,函数的解析式不同).
<x≤m,m<x≤n时,函数的解析式不同).
(1)a的值为;
(2)求出S关于x的函数关系式,并写出x的取值范围.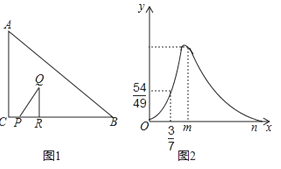
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一外地游客到某特产专营店,准备购买精加工的豆腐乳和猕猴桃果汁两种盒装特产,若购买3盒豆腐乳和2盒猕猴桃果汁共需60元;购买1盒豆腐乳和3盒猕猴桃果汁共需55元.
(1)请分别求出每盒豆腐乳和每盒猕猴桃果汁的价格;
(2)该游客购买了4盒豆腐乳和2盒猕猴桃果汁,共需多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下面的证明
如图,端点为P的两条射线分别交两直线l1、l2于A、C、B、D四点,已知∠PBA=∠PDC,∠l=∠PCD,求证:∠2+∠3=180°.
证明:∵∠PBA=∠PDC( )
∴ (同位角相等,两直线平行)
∴∠PAB=∠PCD( )
∵∠1=∠PCD( )
∴ (等量代换)
∴PC//BF(内错角相等,两直线平行),
∴∠AFB=∠2( )
∵∠AFB+∠3=180°( )
∴∠2+∠3=180°(等量代换)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了计算河的宽度,某学习小组在河对岸选定一个目标点A,再在河岸的这一边选取点B和点C,使AB⊥BC,然后再选取点E,使E C⊥BC,用视线确定BC和AE的交点D.此时如果测得BD=160 米,DC=80米,E C=49米,求A、B间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】A,B,C三名大学生竞选系学生会主席,他们的笔试成绩和口试成绩(单位:分)分别用了两种方式进行了统计,如表和图1:

(1)请将表和图1中的空缺部分补充完整.
(2)竞选的最后一个程序是由本系的300名学生进行投票,三位候选人的得票情况如图2(没有弃权票,每名学生只能推荐一个),则B在扇形统计图中所占的圆心角的度数是.
(3)若每票计1分,系里将笔试、口试、得票三项测试得分按4:3:3的比例确定个人成绩,请计算三位候选人的最后成绩,并根据成绩判断谁能当选.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com