
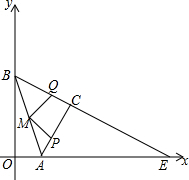
 ƽ��ֱ������ϵxOy�У���֪A��1��0����B��0��3������ABΪб��������ֱ��������ABC����C�ڵ�һ���ޣ�M��AB���е㣮P��Q�ֱ����߶�AC��CB�ϵĶ��㣬��P��A��������$\frac{{\sqrt{5}}}{5}$����λ/s���ٶ���C�˶�����Q��C����������ͬ�ٶ���B�˶���BC��x���ڵ�E�����˶�ʱ��Ϊt s��
ƽ��ֱ������ϵxOy�У���֪A��1��0����B��0��3������ABΪб��������ֱ��������ABC����C�ڵ�һ���ޣ�M��AB���е㣮P��Q�ֱ����߶�AC��CB�ϵĶ��㣬��P��A��������$\frac{{\sqrt{5}}}{5}$����λ/s���ٶ���C�˶�����Q��C����������ͬ�ٶ���B�˶���BC��x���ڵ�E�����˶�ʱ��Ϊt s������ ��1�����ݵ���ֱ�������ε����ʣ��ɵ�CM=AM����MAC=��MCQ������ȫ�������ε��ж������ʣ��ɵô𰸣�
��2������ȫ�������ε��ж������ʣ��ɵ�CF=CD��BF=AD���ɵù���x�ķ��̣�
��3�����ݴ���ϵ�������ɵô𰸣�
��4������ȫ�������ε��ж������ʣ��ɵ�EM��EP�Ĺ�ϵ�����ݹ��ɶ������ɵù���t�ķ��̣�
��� ��1��֤������ͼ1��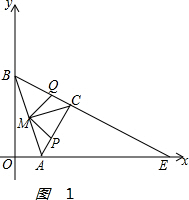 ����CM��
����CM��
�ߡ�ABC�ǵ���ֱ�������Σ�CM��б���ϵ����ߣ�
��CM=AM����MAC=��MCQ=45�㣬
�ڡ�AMP�͡�CMQ�У�
$\left\{\begin{array}{l}{AM=CM}\\{��MAP=��MCQ}\\{AP=CQ}\end{array}\right.$��
���APM�ա�CQM ��SAS����
��MP=MQ��
��2����ͼ2��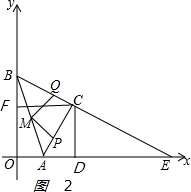 ��C��x�ᡢy��Ĵ��ߣ�����ֱ�ΪD��F
��C��x�ᡢy��Ĵ��ߣ�����ֱ�ΪD��F
��BCF+��ACF=��ACD+��ACF��
���BCF=��ACF��
�ڡ�ACD�͡�BCF�У�
$\left\{\begin{array}{l}{AC=BC}\\{��ADC=��BFC}\\{ACD=��BCF}\end{array}\right.$��
���CBF�ա�CAD��
��CF=CD��BF=AD��
��CF=CD=x����OF=OD=x��
��BF=3-x��AD=x-1��
��3-x=x-1��x=2��
��C��2��2����
��3���������ߵĽ���ʽΪy=ax2+bx+c��
��A��B��C��������룬��
$\left\{\begin{array}{l}{a+b+c=0}\\{c=3}\\{4a+2b+c=0}\end{array}\right.$��
���$\left\{\begin{array}{l}{a=\frac{5}{2}}\\{b=-\frac{11}{2}}\\{c=3}\end{array}\right.$��
�����ߵĽ���ʽΪy=$\frac{5}{2}$x2-$\frac{11}{2}$x+3��
��4�����ڣ�
��ͼ3��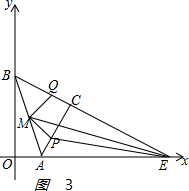 ����EM���ɣ�1��֪��MP=MQ����PMQ=90�㣮
����EM���ɣ�1��֪��MP=MQ����PMQ=90�㣮
����EMP=45�㣬���EMQ=45�㣬���EMP�ա�EMQ������EP=EQ��
��BC�Ľ���ʽΪy=-$\frac{1}{2}$x+3��
��E��6��0����CE=$\sqrt{20}=2\sqrt{5}$��
EQ=2$\sqrt{5}$+t��
��P$��1+\frac{1}{5}t��\frac{2}{5}t��$��
��EP=$\sqrt{{{��5-\frac{1}{5}t��}^2}+{{��\frac{2}{5}t��}^2}}=\sqrt{\frac{1}{5}{t^2}-2t+25}$
��$\sqrt{\frac{1}{5}{t^2}-2t+25}=2\sqrt{5}+\frac{{\sqrt{5}}}{5}t$��
���$t=\frac{5}{6}$
��$t=\frac{5}{6}$��
���� ���⿼���˶��κ����ۺ��⣬������ȫ�������ε��ж������ʣ�����ϵ������������ʽ�����ù��ɶ����ij�����t�ķ����ǽ���ؼ���


 ��ʦָ����ĩ��̾�ϵ�д�
��ʦָ����ĩ��̾�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
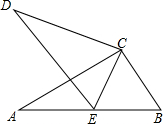 ��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����תһ���ĽǶȵ���DEC��λ�ã���E����AB���ϣ��ҡ�DCB=160�㣬���AED=70�㣮
��ͼ����Rt��ABC��ֱ�Ƕ���C˳ʱ����תһ���ĽǶȵ���DEC��λ�ã���E����AB���ϣ��ҡ�DCB=160�㣬���AED=70�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
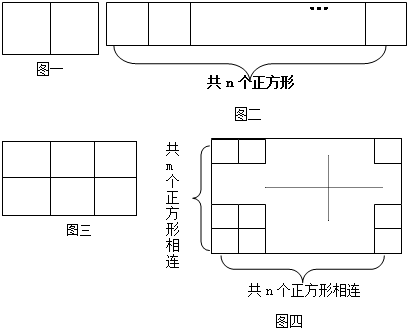
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | x1=4��x2=-4 | B�� | x1=0��x2=-4 | C�� | x1=0��x2=2 | D�� | x1=0��x2=4 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com