
【题目】如图:△ABC中,D点在BC上,现有下列四个命题:①若AB=AC,则∠B=∠C.②若AB=AC,∠BAD=∠CAD,则AD⊥BC,BD=DC.③若AB=AC,BD=DC,则AD⊥BC,∠BAD=∠CAD.④若AB=AC,AD⊥BC,则BD=DC,∠BAD=∠CAD.其中正确的有( ) 
A.1个
B.2个
C.3个
D.4个
科目:初中数学 来源: 题型:
【题目】近年来黔东南州大力发展旅游业,据统计今年上半年全州旅游总收入约29500000000元,将数据29500000000科学记数法表示为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC中,∠B=90°,AB=8cm,BC=6cm,P、Q是△ABC边上的两个动点,其 中点P从点A开始沿A→B方向运动,且速度为每秒1cm,点Q从点B开始沿B→C方向运动,且速度为每秒2cm,它们同时出发,设出发的时间为t秒. 
(1)当t=2秒时,求PQ的长;
(2)求出发时间为几秒时,△PQB是等腰三角形?
(3)若Q沿B→C→A方向运动,则当点Q在边CA上运动时,求能使△BCQ成为等腰三角形的运动时间.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】油桶制造厂的某车间主要负责生产制造油桶用的的圆形铁片和长方形铁片,该车间有工人42人,每个工人平均每小时可以生产圆形铁片120片或者长方形铁片80片.如图,一个油桶由两个圆形铁片和一个长方形铁片相配套. 生产圆形铁片和长方形铁片的工人各为多少人时,才能使生产的铁片恰好配套?
查看答案和解析>>
科目:初中数学 来源: 题型:
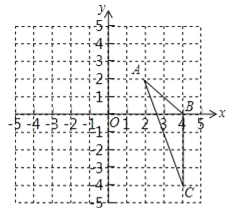
【题目】如图,在平面直角坐标系中,已知△ABC三个顶点的坐标分别是A(2,2),B(4,0),C(4,﹣4)
(1)请画出△ABC向左平移6个单位长度后得到的△A1B1C1;
(2)以点O为位似中心,将△ABC缩小为原来的![]() ,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
,得到△A2B2C2,请在y轴右侧画出△A2B2C2,并求出∠A2C2B2的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面有两个对代数式进行变形的过程:①(c+b)(c-b)-a(a+2b)=c2-b2-a2-2ab=c2-(b2+a2+2ab)=c2-(a+b)2;②(2a2+2)(a2-1)=2(a2+1)(a2-1)=2(a4-1). 其中,完成“分解因式”要求的是( )
A. 只有① B. 只有② C. 有①和② D. 一个也没有
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com