
分析 原式括号中两项通分并利用同分母分式的减法法则计算,同时利用除法法则变形,约分得到最简结果,把a与b的值代入计算即可求出值.
解答 解:原式=[$\frac{(a+b)(a-b)}{(a-b)^{2}}$-$\frac{a(a-b)}{(a-b)^{2}}$]•$\frac{a(a-b)}{{b}^{2}}$=$\frac{b(a-b)}{(a-b)^{2}}$•$\frac{a(a-b)}{{b}^{2}}$=$\frac{a}{b}$,
当a=-1,b=$\sqrt{2}$时,原式=-$\frac{\sqrt{2}}{2}$.
点评 此题考查了分式的化简求值,熟练掌握运算法则是解本题的关键.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:解答题
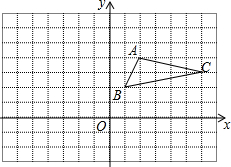 △ABC在平面直角坐标系中的位置如图所示.
△ABC在平面直角坐标系中的位置如图所示.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
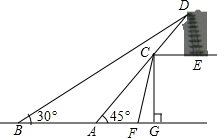 如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.
如图为某风景区中古塔,大坝和湖的截面图,大坝顶端CE和水面平行,点C为大坝顶端拐角处,大坝的坡比i=3:1(即CG:FG=3:1),当小明和同伴从大坝的点F处沿着截面所在方向开始划船,划行20米到达点A处时,他们以仰角45°观察远方,正好看到古塔顶端的点D,且点C在视线AD上,当他们从点A继续沿原方向划船40米,到达点B处时,观察点D的仰角正好为30°.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
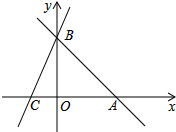 直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.
直线CB:y=3x+b分别与x,y轴交于C(-2,0),B两点,过点B的直线交x轴正半轴于点A,且OB=OA.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | x2-2x-3=x(x-2)-3 | B. | x2-2x-3=(x-1)2-4 | C. | (x+1)(x-3)=x2-2x-3 | D. | x2-2x-3=(x+1)(x-3) |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com