练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】△ABC的三边长分别为a、b、c，下列条件：①∠B=∠C-∠A； ②a2=(b+c)(b-c）；③∠A:∠B:∠C=3:4:5；④a:b:c=5:12:13， 其中能判断△ABC是直角三角形的个数有（ ）

    A.1个B.2个C.3个D.4个

    【答案】C

    【解析】

    根据直角三角形的定义，勾股定理的逆定理一一判断即可．

    :①由∠B=∠C-∠A,∠A+∠B+∠C=180°

    可知：∠B+∠A=180°-∠C=∠C，解得∠C=90°，是直角三角形;

    ②由a2=(b+c)(b-c）,可得，是直角三角形；

    ③由∠A:∠B:∠C=3:4:5，∠A+∠B+∠C=180°

    得∠A=45°，∠B=60°，∠C=75°可知不是直角三角形；

    ④由a:b:c=5:12:13，根据勾股定理的逆定理可知是直角三角形；

    故选：C.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

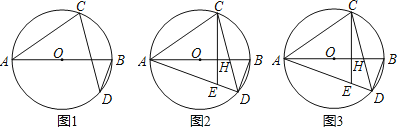
    【题目】如图，AB为⊙O直径，点D为AB下方⊙O上一点，点C为弧ABD中点，连接CD，CA．

    （1）若∠ABD＝α，求∠BDC（用α表示）；

    （2）过点C作CE⊥AB于H，交AD于E，∠CAD＝β，求∠ACE（用β表示）；

    （3）在（2）的条件下，若OH＝5，AD＝24，求线段DE的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某商店购进一批进价为20元/件的日用商品，第一个月，按进价提高50%的价格出售，售出400件；第二个月，商店准备在不低于原售价的基础上进行加价销售，根据销售经验，提高销售单价会导致销售量的减少．销售量y(件)与销售单价x(元)的关系如图所示．

    (1)求y与x之间的函数表达式；

    (2)第二个月的销售单价定为多少元时，可获得最大利润？最大利润是多少？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

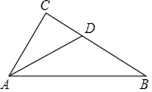
    【题目】已知：如图，在Rt△ABC中，∠C＝90°，∠BAC的角平分线AD交BC边于D．

    （1）以AB边上一点O为圆心，过A、D两点作⊙O，并标出圆心．（不写作法，保留作图痕迹）．

    （2）判断直线BC与⊙O的位置关系，并说明理由．

    （3）若AB＝8，BD＝4，求⊙O的半径．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】第七届世界军人运动会于2019年10月18日至27日在湖北武汉举行，这是中国首次承办世界军人运动会．现有两张纪念卡片分别绘有会徽和吉祥物的图案（如下图），纪念卡背面完全相同．

    （1）小丽从两张纪念卡任意摸一张，则小丽摸到绘有吉祥物“兵兵”的概率为______；

    （2）如果小丽摸两次（第一次摸出后记录并放回），求小丽两次摸到的纪念卡相同的概率．（请用“画树状图”或“列表”等方法写出分析过程）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】按要求解方程：

    （1）直接开平方法： 4(t-3)2=9(2t-3)2

    （2）配方法：2x2-7x-4=0

    （3）公式法： 3x2+5(2x+1)=0

    （4）因式分解法：3(x-5)2=2(5-x)

    （5）abx2-(a2+b2)x+ab=0 (ab≠0)

    （6）用配方法求最值：6x2-x-12

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】《中国诗词大会》以“赏中华诗词，寻文化基因、品生活之美”为基本宗旨，力求通过对诗词知识的比拼及赏析，带动全民重温那些曾经学过的古诗词，分享诗词之美，感受诗词之趣，从古人的智慧和情怀中汲取营养，涵养心灵，自开播以来深受广大师生的喜爱，某中学为了解学校学生的诗词水平，从八、九年级各随机抽取了20名学生进行了测试，并将八、九年级测试成绩(百分制，单位：分)整理如下：收集数据：

    八：93　92　84　55　85　82　66　74　88　67　87　87　67　61　87　61　78　57　72　75

    九：68　66　79　92　86　87　61　86　90　83　90　78　70　67　53　79　86　71　61　89

    整理数据：

    测试成绩x(分)

    年级

    50≤x＜60

    60≤x＜70

    70≤x＜80

    80≤x＜90

    90≤x≤100

    八

    2

    a

    4

    b

    c

    九

    1

    5

    5

    6

    3

    说明：测试成绩x(分)，其中x≥80为优秀，70≤x＜80为良好，60≤x＜70为合格，0≤x＜60为不合格)

    分析数据：

    年级

    平均数

    中位数

    众数

    八

    75.9

    76.5

    d

    九

    77.1

    79

    86

    根据以上信息回答下列问题：

    （1）请直接写出表格中a，b，c，d的值；

    （2）在此次测试中，有位同学的成绩是78分，在他所在的年级属于中等偏上，则这位同学属于哪个年级？请你说明理由；

    （3）若九年级有800名学生，估计九年级诗词水平达到优秀的学生有多少名？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

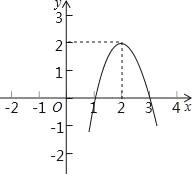
    【题目】二次函数y＝ax2+bx+c（a≠0）的图象如图所示，根据图象解答下列问题：

    （1）写出方程ax2+bx+c＝0的两个根；

    （2）写出不等式ax2+bx+c＞0的解集；

    （3）若方程ax2+bx+c＝k有两个不相等的实数根，求k的取值范围．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，抛物线y=ax2-x+c交x轴于点A和点B（点A在原点的左侧，点B在原点的右侧），点A的坐标为（-3，0），点B的坐标为（1，0），交y轴于点C．

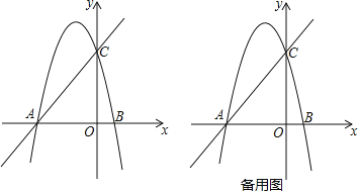
    （1）求该抛物线的解析式；

    （2）已知点P为抛物线上一点，直线PC与x轴交于点Q，使得PQ=CQ，求P点坐标；

    （3）若点M是抛物线对称轴上一点，点N是平面内一点，是否存在以A，C，M，N为顶点的矩形？若存在，请直接写出N点的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案