
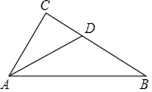
【题目】已知:如图,在Rt△ABC中,∠C=90°,∠BAC的角平分线AD交BC边于D.
(1)以AB边上一点O为圆心,过A、D两点作⊙O,并标出圆心.(不写作法,保留作图痕迹).
(2)判断直线BC与⊙O的位置关系,并说明理由.
(3)若AB=8,BD=4,求⊙O的半径.
【答案】(1)作图见解析;(2)直线BC与⊙O的位置关系为:相切;理由见解析;(3)⊙O的半径为3.
【解析】
(1)以AB边上一点O为圆心,过A、D两点作⊙O,并标出圆心;
(2)根据切线的判定即可判断直线BC与⊙O的位置关系;
(3)根据AB=8,BD=4,即可求⊙O的半径.
(1)如图,⊙O即为所求;
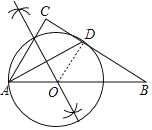
(2)直线BC与⊙O的位置关系为:相切,理由如下:
连接OD,
∴OD=OA,
∴∠OAD=∠ODA,
∵AD平分∠BAC,
∴∠BAD=∠CAD,
∴∠ODA=∠CAD,
∴AC∥OD,
∴∠ODB=∠C=90°,
∴OD⊥BC,OD是半径,
∴直线BC与⊙O相切;
(3)设⊙O的半径为x,
在Rt△OBD中,OD=x,OB=8﹣x,BD=4,
∴(8﹣x)2=x2+42,
解得x=3.
答:⊙O的半径为3.


科目:初中数学 来源: 题型:
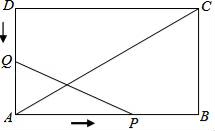
【题目】如图,在矩形ABCD中,AB=12cm,BC=6cm,点P沿AB边从点A开始向点B以2cm/s的速度移动,点Q沿DA边从点D开始向点A以1cm/s的速度移动,如果P、Q同时出发,用t(s)表示移动的时间(0≤t≤6),那么:
(1)当t为何值时,△QAP是等腰直角三角形?
(2)当t为何值时,以点Q、A、P为顶点的三角形与△ABC相似?
查看答案和解析>>
科目:初中数学 来源: 题型:
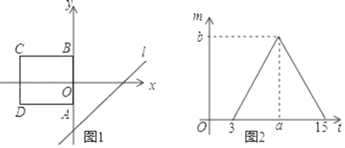
【题目】如图1,正方形ABCD在直角坐标系中,其中AB边在y轴上,其余各边均与坐标轴平行,直线l:y=x﹣5沿y轴的正方向以每秒1个单位的速度平移,在平移的过程中,该直线被正方形ABCD的边所截得的线段长为m,平移的时间为t(秒),m与t的函数图象如图2所示,则图2中b的值为( )
A.3![]() B.5
B.5![]() C.6
C.6![]() D.10
D.10![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小昕的口袋中有5把相似的钥匙,其中2把钥匙(记为A1,A2)能打开教室前门锁,而剩余的3把钥匙(记为B1,B2,B3)不能打开教室前门锁.
(1)小昕从口袋中随便摸出一把钥匙就能打开教室前门锁的概率是 ;
(2)请用树状图或列表等方法,求出小昕从口袋中第一次随机摸出的一把钥匙不能打开教室前门锁(摸出的钥匙不再放回),而第二次随机摸出的一把钥匙正好能打开教室前门锁的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是半圆O的直径,点D在半圆O上,AB=13,AD=5,C是弧BD上的一个动点,连接AC,过D点作DH⊥AC于H.连接BH,在点C移动的过程中,BH的最小值是( )

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC的三边长分别为a、b、c,下列条件:①∠B=∠C-∠A; ②a2=(b+c)(b-c);③∠A:∠B:∠C=3:4:5;④a:b:c=5:12:13, 其中能判断△ABC是直角三角形的个数有( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
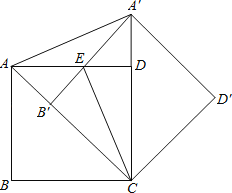
【题目】如图,把正方形ABCD绕点C按顺时针方向旋转45°得到正方形A′B′CD′(此时,点B′落在对角线AC上,点A′落在CD的延长线上),A′B′交AD于点E,连接AA′、CE.
求证:(1)△ADA′≌△CDE;
(2)直线CE是线段AA′的垂直平分线.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com