
����Ŀ�����й�ʫ�ʴ�ᡷ�������л�ʫ�ʣ�Ѱ�Ļ�����Ʒ����֮����Ϊ������ּ������ͨ����ʫ��֪ʶ�ı�ƴ������������ȫ��������Щ����ѧ���Ĺ�ʫ�ʣ�����ʫ��֮��������ʫ��֮Ȥ���ӹ��˵��ǻۺ��黳�м�ȡӪ�����������飬�Կ����������ܹ��ʦ����ϲ����ij��ѧΪ�˽�ѧУѧ����ʫ��ˮƽ���Ӱˡ����꼶�������ȡ��20��ѧ�������˲��ԣ������ˡ����꼶���Գɼ�(�ٷ��ƣ���λ����)�������£��ռ����ݣ�
�ˣ�93��92��84��55��85��82��66��74��88��67��87��87��67��61��87��61��78��57��72��75
�ţ�68��66��79��92��86��87��61��86��90��83��90��78��70��67��53��79��86��71��61��89
�������ݣ�
���Գɼ�x(��) �꼶 | 50��x��60 | 60��x��70 | 70��x��80 | 80��x��90 | 90��x��100 |
�� | 2 | a | 4 | b | c |
�� | 1 | 5 | 5 | 6 | 3 |
˵�������Գɼ�x(��)������x��80Ϊ���㣬70��x��80Ϊ���ã�60��x��70Ϊ�ϸ�0��x��60Ϊ���ϸ�)
�������ݣ�
�꼶 | ƽ���� | ��λ�� | ���� |
�� | 75.9 | 76.5 | d |
�� | 77.1 | 79 | 86 |
����������Ϣ�ش��������⣺
��1����ֱ��д��������a��b��c��d��ֵ��
��2���ڴ˴β����У���λͬѧ�ijɼ���78�֣��������ڵ��꼶�����е�ƫ�ϣ�����λͬѧ�����ĸ��꼶������˵�����ɣ�
��3�������꼶��800��ѧ�������ƾ��꼶ʫ��ˮƽ�ﵽ�����ѧ���ж�������
���𰸡���1��a=5��b=7��c=2��d=87����2����λͬѧ���ڰ��꼶�����ɼ���������3�����꼶ʫ��ˮƽ�ﵽ�����ѧ����360��
��������
��1�����ݸ��������ݼ���д��������a��b��c��d��ֵ��
��2��������λ���������ɣ�
��3�����������������ѧ����ռ�������㼴�ɣ�
�⣺��1���Ѱ��꼶�IJ��Գɼ���С��������Ϊ��55��57��61��61��66��67��67��72��74��75��78��82��84��85��87��87��87��88��92��93��
��60��x��70����5�ˣ���a=5��
80��x��90����7�ˣ���b=7��
90��x��100����2�ˣ���c=2��
����������87��������Ϊ87�֣���d=87
��2���߰��꼶����λ��Ϊ76.5�֣����꼶����λ��Ϊ79�֣�
78��76.5
���ڴ˴β����У���λͬѧ�ijɼ���78�֣��������ڵ��꼶�����е�ƫ�ϣ�����λͬѧ���ڰ��꼶��
��3�����꼶��������Ϊ9��
��![]() ���ˣ�
���ˣ�
�𣺾��꼶ʫ��ˮƽ�ﵽ�����ѧ����360��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ������֪���κ���y=ax2+bx+c��a��0����ͼ����ͼ��ʾ�����н��ۣ���abc��0����2a+b��0����b2��4ac��0����a��b+c��0��������ȷ�ĸ����ǣ�������
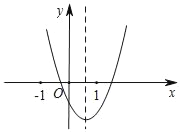
A. 1 B. 2 C. 3 D. 4
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ������D�ڰ�ԲO�ϣ�AB��13��AD��5��C�ǻ�BD�ϵ�һ�����㣬����AC����D����DH��AC��H������BH���ڵ�C�ƶ��Ĺ����У�BH����Сֵ�ǣ� ��

A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ABC�����߳��ֱ�Ϊa��b��c�������������١�B=��C-��A�� ��a2=(b+c)(b-c�����ۡ�A:��B:��C=3:4:5����a:b:c=5:12:13�� �������ж���ABC��ֱ�������εĸ����У� ��
A.1��B.2��C.3��D.4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������ABCD�У���E��BC���е㣬��CΪԲ�ġ�CEΪ�뾶��������CD�ڵ�F������AE��AF����AB=2����B=60��������Ӱ���ֵ����Ϊ(����)
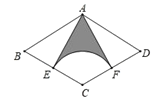
A.![]()
![]() B.
B.![]()
![]()
C.2![]() �C��D.2
�C��D.2![]()
![]()
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֽ���й����е��������.����ͼ��ʾ���ĸ���ֽͼ����.������Գ�ͼ���������ĶԳ�ͼ�ε��ǣ� ��
A.  B.
B.  C.
C.  D.
D. 
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��������y=![]() x2+bx+c��ֱ��y=
x2+bx+c��ֱ��y=![]() x+3����A��B���㣬��x����C��D���㣬����AC��BC����֪A��0��3����C����3��0����
x+3����A��B���㣬��x����C��D���㣬����AC��BC����֪A��0��3����C����3��0����
��1���������ߵĽ���ʽ��
��2���������߶Գ���l����һ��M��ʹ|MB��MD|��ֵ������������ֵ��
��3����PΪy���Ҳ���������һ���㣬����PA������P��PQ��PA��y���ڵ�Q���ʣ��Ƿ���ڵ�Pʹ����A��P��QΪ���������������ABC���ƣ������ڣ���������з��������ĵ�P�����ꣻ�������ڣ���˵�����ɣ�
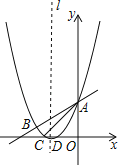
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪�������� y��ax2��bx��1 ���� A(1��0)��B(��1��3)���㣮
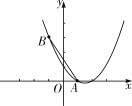
��1���� a��b ��ֵ��
��2�����߶� AB Ϊ���������� ABB��A�����ܷ���֪������ƽ�ƣ�ʹ�侭�� A����B�����㣿���ܣ����ƽ�ƺ� A����B������������ߵĽ���ʽ�������ܣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���ס������˷ֱ��A��B����ͬʱ������������У�����ǰ��B�ء�A�أ���������ʱͣ����4min���ָ���ԭ��ǰ��Ŀ�ĵأ��ס�������֮��ľ���y(m)�������ʱ��x(min) ֮��ĺ�����ϵ��ͼ��ʾ��������˵���� ��A��B֮��ľ���Ϊ1200m���ڼ����ߵ��ٶ����ҵ�1��5������![]() ����
����![]() �����Ͻ�����ȷ����( )
�����Ͻ�����ȷ����( )

A.�٢�B.�٢ڢ�C.�٢ۢ�D.�٢ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com