
【题目】已知:抛物线 y=ax2+bx+1 经过 A(1,0)、B(-1,3)两点.
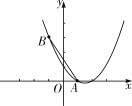
(1)求 a,b 的值;
(2)以线段 AB 为边作正方形 ABB′A′,能否将已知抛物线平移,使其经过 A′、B′两点?若能,求出平移后经过 A′、B′两点的抛物线的解析式;若不能,请说明理由.
【答案】(1)![]() ,
,![]() ;(2)能,抛物线解析式为:
;(2)能,抛物线解析式为:![]() 或
或![]() .
.
【解析】
(1)根据题意将A、B两点坐标代入解析式进一步求解即可;
(2)如图,根据题意,首先画出合适的图形,得出正方形ABB′A′以及ABB′′A′′,然后根据两种图形分两种情况进一步分析讨论即可.
(1)∵抛物线 y=ax2+bx+1 经过 A(1,0)、B(-1,3)两点,
故有:![]() ,
,![]() ,
,
∴![]() ,
,![]() ;
;
(2)
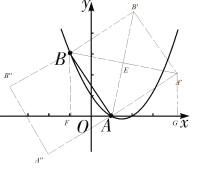
连接A′B,AB′交于点E,过点B作BF⊥x轴于点F,过点A′作A′G⊥x轴于点G,
∵四边形ABB′A′为正方形,
∴∠BA A′=90°,AB= A′A,BE= A′E= B′E=AE,
∵∠BA A′=90°,
∴∠BAF+∠A′AG=90°,
∵∠ABF+∠BAF=90°,
∴∠A′AG=∠ABF,
在△BAF与△A′AG中,
∵∠BFA=∠AG A′,∠ABF=∠A′AG,AB= A′A,
∴△BAF≌△A′AG,
∴A′G=AF,AG=BF,
∵AF=2,BF=3,
∴点A′的横坐标=OG=OA+AG=4,
点A′的纵坐标= A′G=2,
即点A′的坐标为(4,2),
∵点A′的坐标为(4,2),点B的坐标为(![]() ,3),E是A′B的中点,
,3),E是A′B的中点,
∴点E的坐标为:(![]() ,
,![]() ),
),
∵E是A B′的中点,点A的坐标为(1,0),
∴点B′的横坐标=![]() ,点B′的纵坐标=
,点B′的纵坐标=![]() ,
,
即点B′的坐标为(2,5),
过A、B两点的抛物线的解析式为:![]() ,
,
化为顶点式为:![]() ,
,
设平移后的解析式为:![]() ,
,
假设其经过点A′、B′,
则:![]() ,
,
![]() ,
,
∴![]() ,
,![]() ,
,
故存在经过A′、B′两点的抛物线,其解析式为:![]() ,
,
当正方形为ABB′′A′′时,同理可得点A′′的坐标为(![]() ,
,![]() ),点B′′的坐标为(
),点B′′的坐标为(![]() ,1),
,1),
此时经过A′′、B′′两点的抛物线的解析式为:![]() .
.


科目:初中数学 来源: 题型:
【题目】某商店购进一批进价为20元/件的日用商品,第一个月,按进价提高50%的价格出售,售出400件;第二个月,商店准备在不低于原售价的基础上进行加价销售,根据销售经验,提高销售单价会导致销售量的减少.销售量y(件)与销售单价x(元)的关系如图所示.
(1)求y与x之间的函数表达式;
(2)第二个月的销售单价定为多少元时,可获得最大利润?最大利润是多少?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】《中国诗词大会》以“赏中华诗词,寻文化基因、品生活之美”为基本宗旨,力求通过对诗词知识的比拼及赏析,带动全民重温那些曾经学过的古诗词,分享诗词之美,感受诗词之趣,从古人的智慧和情怀中汲取营养,涵养心灵,自开播以来深受广大师生的喜爱,某中学为了解学校学生的诗词水平,从八、九年级各随机抽取了20名学生进行了测试,并将八、九年级测试成绩(百分制,单位:分)整理如下:收集数据:
八:93 92 84 55 85 82 66 74 88 67 87 87 67 61 87 61 78 57 72 75
九:68 66 79 92 86 87 61 86 90 83 90 78 70 67 53 79 86 71 61 89
整理数据:
测试成绩x(分) 年级 | 50≤x<60 | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x≤100 |
八 | 2 | a | 4 | b | c |
九 | 1 | 5 | 5 | 6 | 3 |
说明:测试成绩x(分),其中x≥80为优秀,70≤x<80为良好,60≤x<70为合格,0≤x<60为不合格)
分析数据:
年级 | 平均数 | 中位数 | 众数 |
八 | 75.9 | 76.5 | d |
九 | 77.1 | 79 | 86 |
根据以上信息回答下列问题:
(1)请直接写出表格中a,b,c,d的值;
(2)在此次测试中,有位同学的成绩是78分,在他所在的年级属于中等偏上,则这位同学属于哪个年级?请你说明理由;
(3)若九年级有800名学生,估计九年级诗词水平达到优秀的学生有多少名?
查看答案和解析>>
科目:初中数学 来源: 题型:
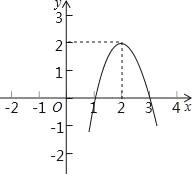
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,根据图象解答下列问题:
(1)写出方程ax2+bx+c=0的两个根;
(2)写出不等式ax2+bx+c>0的解集;
(3)若方程ax2+bx+c=k有两个不相等的实数根,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
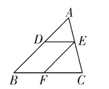
【题目】如图,在△ABC 中,D、E、F 分别为边 AB、AC、BC 上的点,连接 DE、EF.若 DE∥BC,EF∥AB,则图中共有________对相似三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了解某校九年级男生的体能情况,体育老师从中随机抽取部分男生进行引体向上测试,并对成绩进行了统计,绘制成尚不完整的扇形图和条形图,根据图形信息回答下列问题:
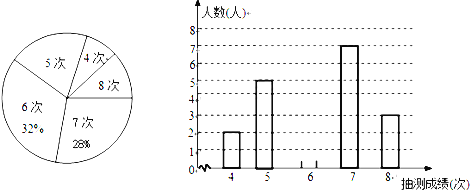
(1)本次抽测的男生有________人,抽测成绩的众数是_________;
(2)请将条形图补充完整;
(3)若规定引体向上6次以上(含6次)为体能达标,则该校125名九年级男生中估计有多少人体能达标?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() 的部分对应值如下表:
的部分对应值如下表:
x | … | -3 | -2 | 0 | 3 | 5 | … |
y | … | 7 | 0 | -8 | -5 | 7 | … |
则以下四个结论:①图象的开口向上;②函数的最小值为-8;③方程![]() 的两根分别-2,4;④若y<-5,则-1<x<3.其中正确结论的个数是( )
的两根分别-2,4;④若y<-5,则-1<x<3.其中正确结论的个数是( )
A.1个B.2个C.3个D.4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=ax2-![]() x+c交x轴于点A和点B(点A在原点的左侧,点B在原点的右侧),点A的坐标为(-3,0),点B的坐标为(1,0),交y轴于点C.
x+c交x轴于点A和点B(点A在原点的左侧,点B在原点的右侧),点A的坐标为(-3,0),点B的坐标为(1,0),交y轴于点C.
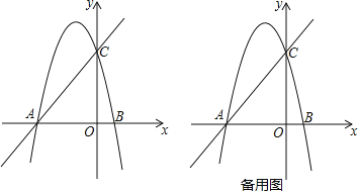
(1)求该抛物线的解析式;
(2)已知点P为抛物线上一点,直线PC与x轴交于点Q,使得PQ=![]() CQ,求P点坐标;
CQ,求P点坐标;
(3)若点M是抛物线对称轴上一点,点N是平面内一点,是否存在以A,C,M,N为顶点的矩形?若存在,请直接写出N点的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
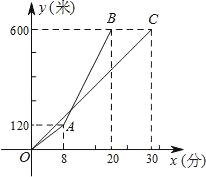
【题目】甲、乙两人沿同一路线登山,图中线段OC、折线OAB分别是甲、乙两人登山的路程y(米)与登山时间x(分)之间的函数图象.请根据图象所提供的信息,解答如下问题:
(1)求甲登山的路程与登山时间之间的函数关系式,并写出自变量x的取值范围;
(2)求乙出发后多长时间追上甲?此时乙所走的路程是多少米?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com